题目内容
【题目】如图所示,圆锥的顶点为A,底面的圆心为O,BC是底面圆的一条直径,点D,E在底面圆上,已知![]() ,
,![]() .
.
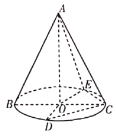
(1)证明:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求直线OC与平面ACE所成角的正弦值.
,求直线OC与平面ACE所成角的正弦值.
【答案】(1)证明见解析(2)![]() .
.
【解析】
(1)由![]() 可得
可得![]() ,易证
,易证![]() 平面OAC,即可求得
平面OAC,即可求得![]() (2)建立空间直角坐标系,利用线面角计算公式求解即可.
(2)建立空间直角坐标系,利用线面角计算公式求解即可.
(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() .
.
在圆锥AO中,AO与底面垂直,
所以![]() .
.
因为![]() ,
,
所以![]() 平面OAC,
平面OAC,
因为![]() 平面OAC,
平面OAC,
所以![]() .
.
(2)由(1)可知0A,OC,OD两两垂直,以O为原点建立如图所示的空间直角坐标系.

则![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角,
的平面角,
所以![]() ,从而可得
,从而可得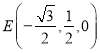 .
.
所以![]() ,
,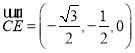 ,
,![]() .
.
设平面ACE的法向量为![]() .
.
则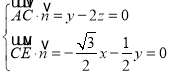 .令
.令![]() ,则
,则 .
.
设直线OC与平面ACE所成的角为![]() ,
,
则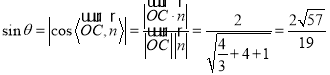 .
.

【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 800 |
不满意 | 300 | 200 | 400 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤
【题目】某手机公司生产某款手机,如果年返修率不超过千分之一,则生产部门当年考核优秀,现获得该公司2010-2018年的相关数据如下表所示:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产量(万台) | 3 | 4 | 5 | 6 | 7 | 7 | 9 | 10 | 12 |
产品年利润(千万元) | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.8 | 7.5 | 7.9 | 9.1 |
年返修量(台) | 47 | 42 | 48 | 50 | 92 | 83 | 72 | 87 | 90 |
(1)从该公司2010-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (千万元)关于年生产量
(千万元)关于年生产量![]() (万台)的线性回归方程(精确到0.01).部分计算结果:
(万台)的线性回归方程(精确到0.01).部分计算结果:![]() ,
,![]() ,
,![]() .
.
附: ;线性回归方程
;线性回归方程![]() 中,
中, ,
,![]() .
.