Question

【题目】已知函数为自然对数的底数）．

（1）若曲线在点（处的切线与曲线在点处的切线互相垂直，求函数在区间上的最大值；

（2）设函数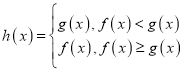，试讨论函数零点的个数．

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）分别求出y=f（x）与y=g（x）在x=0处的导数，利用斜率之积等于-1求得，得到f（x）解析式，再由导数判断f（x）在区间[-1，1]上单调递减，从而求得最大值；

（2）函数在R上单调递增，仅在x=1处有一个零点，且x＜1时，g（x）＜0，再由导数分类判定f（x）的零点情况，则答案可求．

（1）∵f′（x）=-3x2+a，g′（x）=ex，

∴f′（0）=a，g′（0）=1，

由题意知，，f（x）在区间[-1，1]上单调递减，

∴；

（2）函数g（x）=ex-e在R上单调递增，仅在x=1处有一个零点，且x＜1时，g（x）＜0，

又f′（x）=-3x2+a．

①当a≤0时，f′（x）≤0，f（x）在R上单调递减，且过点（0，-），f（-1）=＞0．

即f（x）在x≤0时，必有一个零点，此时y=h（x）有两个零点；

②当a＞0时，令f′（x）=-3x2+a=0，解得＜0，＞0．

则是函数f（x）的一个极小值点，是函数f（x）的一个极大值点．

而f（-）=＜0，

现在讨论极大值的情况：

f（）=．

当f（）＜0，即a＜时，函数f（x）在（0，+∞）上恒小于0，此时y=h（x）有两个零点；

当f（）=0，即a=时，函数f（x）在（0，+∞）上有一个零点，，此时y=h（x）有三个零点；

当f（）＞0，即a＞时，函数f（x）在（0，+∞）上有两个零点，一个零点小于，一个零点大于．

若f（1）=a-＜0，即a＜时，y=h（x）有四个零点；

f（1）=a=0，即a=时，y=h（x）有三个零点；

f（1）=a-＞0，即a＞时，y=h（x）有两个零点．

综上所述，当a＜或a＞时，y=h（x）有两个零点；当a=或a=时，y=h（x）有三个零点；当＜a＜时，y=h（x）有四个零点．