题目内容
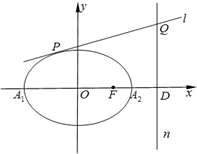
如图,椭圆C1:
+
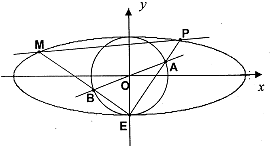
=1(a>b,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆Cl的长轴三等分,且圆C2的面积为π.椭圆Cl的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)(i)设PM的斜率为t,直线l斜率为K1,求
的值;
(ii)求△EPM面积最大时直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)(i)设PM的斜率为t,直线l斜率为K1,求
| K1 |
| t |
(ii)求△EPM面积最大时直线l的方程.

(Ⅰ)∵圆C2:x2+y2=b2的面积为π,
∴b2π=π,即b=1.
∴a=3b=3,
椭圆方程为
+y2=1;
(Ⅱ)(i)由题意知直线PE、ME的斜率存在且不为0,PE⊥EM,
不妨设直线PE的斜率为k(k>0),则PE:y=kx-1,
由
,得
或
.
∴P(
,
),
用-
去代k,得M(
,
),则
t=kPM=
=
.
由
,得
或
.
∴A(
,
).
∴K1=
,则
=
=5;
(ii)|PE|=
=
,
|EM|=
=
.
∴S△EPM=
•
•
=
=
=
.
设
+k=u,
则S△EPM=
=
≤
=
.
当且仅当
+k=u=
时取等号,
此时(k-
)2=(k+
)2-4=
,
∴k-
=±
.
则直线AB:y=
x.
∴所求的直线l的方程为:y=±
x.
∴b2π=π,即b=1.
∴a=3b=3,
椭圆方程为
| x2 |
| 9 |
(Ⅱ)(i)由题意知直线PE、ME的斜率存在且不为0,PE⊥EM,
不妨设直线PE的斜率为k(k>0),则PE:y=kx-1,
由
|
|
|
∴P(
| 18k |
| 9k2+1 |
| 9k2-1 |
| 9k2+1 |
用-
| 1 |
| k |
| -18k |
| k2+9 |
| 9-k2 |
| k2+9 |
t=kPM=
| ||||
|
| k2-1 |
| 10k |
由
|
|
|
∴A(
| 2k |
| 1+k2 |
| k2-1 |
| k2+1 |
∴K1=
| k2-1 |
| 2k |
| K1 |
| t |
| ||
|
(ii)|PE|=
(
|
| 18k |
| 9k2+1 |
| 1+k2 |
|EM|=
| ||
|
1+
|
| 18 |
| 9+k2 |
| 1+k2 |
∴S△EPM=
| 1 |
| 2 |
| 18k |
| 9k2+1 |
| 1+k2 |
| 18 |
| 9+k2 |
| 1+k2 |
=
| 162k(1+k2) |
| (9+k2)(1+9k2) |
| 162(k+k3) |
| 9k4+82k2+9 |
=
162(
| ||
9k2+82+
|
设
| 1 |
| k |
则S△EPM=
| 162u |
| 82+9(u2-2) |
| 162 | ||
9u+
|
| 162 | ||||
2
|
| 27 |
| 8 |
当且仅当
| 1 |
| k |
| 8 |
| 3 |
此时(k-
| 1 |
| k |
| 1 |
| k |
| 28 |
| 9 |
∴k-
| 1 |
| k |
2
| ||
| 3 |
则直线AB:y=
| k2-1 |
| 2k |
∴所求的直线l的方程为:y=±
| ||
| 3 |

练习册系列答案
相关题目