题目内容

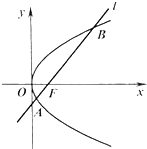
已知点A（1，0），定直线l：x=-1，B为l上的一个动点，过B作直线m⊥l，连接AB，作线段AB的垂直平分线n，交直线m于点M．
（1）求点M的轨迹C的方程；
（2）过点N（4，0）作直线h与点M的轨迹C相交于不同的两点P，Q，求证OP⊥OQ（O为坐标原点）．
（1）由已知|MA|=|MB|
∴M的轨迹为以A为焦点，l为准线的抛物线．
∴M的轨迹方程为y2=4x．
（2）当h⊥x时，h：x=4由
x=4
y2=4x
得y=±4
此时，P（4，4），Q（4，-4）
KOP=1，KOQ=-1∴OP⊥OQ
当h与x轴不垂直时，设l：y=k（x-4）
由
y=k(x-4)
y2=4x
得k2x2-（8k2+4）x+16k2=0
x1?x2=16，y1?y2=-
x11
?
x22
=-16
∴
OA
•
OB
=x1?x2+y1?y2=0
∴OP⊥OQ
练习册系列答案
相关题目
在平面直角坐标系xOy中，△ABC的顶点B、C的坐标为B（-2，0），C（2，0），直线AB，AC的斜率乘积为-
1
4
，设顶点A的轨迹为曲线E．
（1）求曲线E的方程；
（2）设曲线E与y轴负半轴的交点为D，过点D作两条互相垂直的直线l1，l2，这两条直线与曲线E的另一个交点分别为M，N．设l1的斜率为k（k≠0），△DMN的面积为S，试求
S
|k|
的取值范围．
如图，已知抛物线C：y2=4x焦点为F，直线l经过点F且与抛物线C相交于A，B两点
（Ⅰ）若线段AB的中点在直线y=1上，求直线l的方程；
（Ⅱ）若线段|AB|=20，求直线l的方程．
如图所示，设点F坐标为（1，0），点P在y轴上运动，点M在x轴运动上，其中
PM
•
PF
=0，若动点N满足条件
PN
=
MP

（Ⅰ）求动点N的轨迹E的方程；
（Ⅱ）过点F（1，0）的直线l和l′分别与曲线E交于A、B两点和C、D两点，若l⊥l′，试求四边形ACBD的面积的最小值．
如图，椭圆C1：
x2
a2
+
y2
b2
=1（a＞b，b＞0）和圆C2：x2+y2=b2，已知圆C2将椭圆Cl的长轴三等分，且圆C2的面积为π．椭圆Cl的下顶点为E，过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B，直线EA、EB与椭圆C1的另一个交点分别是点P、M．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）（i）设PM的斜率为t，直线l斜率为K1，求
K1
t
的值；
（ii）求△EPM面积最大时直线l的方程．
设P（x0，y0）是抛物线y2=2px（p＞0）上异于顶点的定点，A（x1，y1），B（x2，y2）是抛物线上的两个动点，且直线PA与PB的倾斜角互补
（1）求
y1+y2
y0
的值
（2）证明直线AB的斜率是非零常数．
已知平面内一动点P到点F（2，0）的距离比点P到y轴的距离大2，
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ）过点F且斜率为2
2
的直线交轨迹C于A（x1，y1），B（x2，y2）（x1＜x2）两点，P（x3，y3）（x3≥0）为轨迹C上一点，若
OP
=
OA
+λ
OB
，求λ的值．
已知圆C：x2+y2-2x+4y-4=0，
（Ⅰ）若过定点（-2，0）的直线l与圆C相切，求直线l的方程；
（Ⅱ）若过定点（-1，0）且倾斜角为
π
6
的直线l与圆C相交于A，B两点，求线段AB的中点P的坐标．
直线与双曲线x2-4y2=4交于A、B两点，若线段AB的中点坐标为（8，1），则直线的方程为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网