��Ŀ����
��ͼ����֪��ԲC��
+
=1(a��b��0)����������
��A1��A2�ֱ�����ԲC�������������㣬��F����ԲC���ҽ��㣮��D��x����λ��A2�Ҳ��һ�㣬������
+
=
=2��
��1������ԲC�ķ����Լ���D�����ꣻ
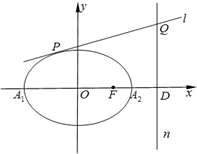
��2������D��x��Ĵ���n������ֱ��l��y=kx+m����ԲC���ҽ���һ��������P��ֱ��l��ֱ��n�ڵ�Q����֤�����߶�PQΪֱ����Բ������㣬�������������꣮
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| |A1D| |
| 1 |
| |A2D| |
| 2 |
| |FD| |
��1������ԲC�ķ����Լ���D�����ꣻ
��2������D��x��Ĵ���n������ֱ��l��y=kx+m����ԲC���ҽ���һ��������P��ֱ��l��ֱ��n�ڵ�Q����֤�����߶�PQΪֱ����Բ������㣬�������������꣮

��1��A1��-a��0����A2��a��0����F��c��0������D��x��0����
��
+
=2��
+
=2��
��|FD|=1����x-c=1����x=c+1��
����
+
=2��
��c+1=��c+1+a����c+1-a����
�֡�
=
⇒a=
c����c+1=(c+1+
c)(c+1-
c)��
��c2-c=0����c��0����c=1��
��a=
��b=1��
����ԲC��
+y2=1����D��2��0����
��2��֤������Q��2��2k+m������P��x0��y0����
��
⇒
+(kx+m)2=1⇒x2+2��kx+m��2=2⇒��2k2+1��x2+4kmx+2m2-2=0��
���ڡ�=16k2m2-4��2k2+1����2m2-2��=0⇒2k2-m2+1=0⇒m2=2k2+1��*����
����Τ�ﶨ����2x0=
��
��x0=
��
�ɣ�*���ɵ�
=-
����y0=kx0+m=-
+m=
����P(-
��
)��
�����߶�PQΪֱ����Բ������һ��M��x��y����
��
•
=0��(x+
)(x-2)+(y-
)(y-(2k+m))=0⇒x2+y2+(
-2)x+(2k+m+
)y+(1-
)=0��
�ɶԳ���֪������x���ϣ���y=0��ȡAʱ������ʽ���ʹ�����C��
��
| 1 |
| |A1D| |
| 1 |
| |A2D| |
| 1 |
| x+a |
| 1 |
| x-a |
��|FD|=1����x-c=1����x=c+1��
����
| 1 |
| c+1+a |
| 1 |
| c+1-a |
��c+1=��c+1+a����c+1-a����
�֡�
| c |
| a |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
��c2-c=0����c��0����c=1��
��a=
| 2 |
����ԲC��
| x2 |
| 2 |
��2��֤������Q��2��2k+m������P��x0��y0����
��
|
| x2 |
| 2 |
���ڡ�=16k2m2-4��2k2+1����2m2-2��=0⇒2k2-m2+1=0⇒m2=2k2+1��*����
����Τ�ﶨ����2x0=
| -4km |
| 2k2+1 |
��x0=
| -2km |
| 2k2+1 |
�ɣ�*���ɵ�
| -2km |
| m2 |
| 2k |
| m |
| 2k2 |
| m |
| 1 |
| m |
| 2k |
| m |
| 1 |
| m |
�����߶�PQΪֱ����Բ������һ��M��x��y����
��
| MP |
| MQ |
| 2k |
| m |
| 1 |
| m |
| 2k |
| m |
| 1 |
| m |
| 2k |
| m |
�ɶԳ���֪������x���ϣ���y=0��ȡAʱ������ʽ���ʹ�����C��

��ϰ��ϵ�д�
�����Ŀ