Question

【题目】已知椭圆的离心率为，且抛物线的焦点恰好是椭圆的一个焦点.

（Ⅰ）求椭圆的方程；

（Ⅱ）过点作直线与椭圆交于，两点，点满足（为坐标原点），求四边形面积的最大值，并求此时直线的方程.

Answer 1

【答案】（1）；（2）平行四边形OANB的面积最大值为2，直线的方程为.

【解析】

试题本题主要考查椭圆的标准方程和几何性质、抛物线的标准方程和几何性质、直线与椭圆相交问题等基础知识，意在考查考生的分析问题解决问题的能力、运算求解能力. 第一问，利用椭圆的离心率和抛物线的焦点坐标列出方程，解出a,b,c的值，从而得到椭圆的标准方程；第二问，对直线的斜率进行讨论，当斜率存在时，将直线方程与椭圆方程联立，消参，得到关于x的方程，利用韦达定理，得到和代入到中，通过换元法再利用均值不等式求出最大值，从而得到直线方程.

试题解析：（Ⅰ）设椭圆的焦距为，∵离心率为，∴，∴，又点是抛物线的焦点，∴，∴椭圆C的方程为. 4分

（Ⅱ）∵，∴四边形OANB为平行四边形，当直线的斜率不存在时，显然不符合题意；

当直线的斜率存在时，设直线的方程为，直线与椭圆于、两点，由.

由 . 6分

，， 7分

∵，

∴

， 9分

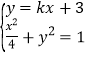
令，则（由上式知），

∴，

当且仅当，即时取等号，

∴当时，平行四边形OANB的面积最大值为2.

此时直线的方程为. 12分