题目内容
【题目】设二次函数![]() 满足下列条件:当
满足下列条件:当![]() 时,
时,![]() 的最小值为0,且
的最小值为0,且![]() 成立;当
成立;当![]() 时,
时,![]() 恒成立.
恒成立.
(1)求![]() 的解析式;
的解析式;
(2)若对![]() ,不等式
,不等式![]() 恒成立、求实数
恒成立、求实数![]() 的取值范围;
的取值范围;
(3)求最大的实数![]() ,使得存在实数
,使得存在实数![]() ,只要当
,只要当![]() 时,就有
时,就有![]() 成立.
成立.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)9.
;(3)9.
【解析】
(1)由![]() 知函数图象的对称轴是
知函数图象的对称轴是![]() ,最小值为0,因此顶点为
,最小值为0,因此顶点为![]() ,这样函数解析式可写为
,这样函数解析式可写为![]() ,在不等式
,在不等式![]() 令
令![]() 得
得![]() ,从而有
,从而有![]() ,由此可求得
,由此可求得![]() ;
;
(2)不等式![]() 化为
化为![]() ,当
,当![]() 时,应有
时,应有![]() ,当
,当![]() ,应有
,应有![]() .由此可得
.由此可得![]() 的取值范围;
的取值范围;
(3)由![]() ,即
,即![]() 的图象与直线
的图象与直线![]() 切于点
切于点![]() ,因此把
,因此把![]() 的图象向右平移,就有一部分满足
的图象向右平移,就有一部分满足![]() ,由此可找到
,由此可找到![]() 的最大值.
的最大值.
解:(1)由题意,函数的顶点坐标为![]() ,
,
解析式可设为![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
经检验,当![]() 时,
时,![]() 恒成立,
恒成立,
∴函数解析式为![]() .
.
(2)不等式变形为:![]() ,
,
令![]() ,对称轴为
,对称轴为![]() ,
,
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调增,∴
上单调增,∴![]() ,解得
,解得![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴![]() .
.
综上所述![]() .
.
(本小问也可用分离参数的方法来求![]()
![]() )
)
(3)当![]() 时,
时,![]() 与
与![]() 相切于点
相切于点![]() ,向右平移
,向右平移![]() 的过程中,
的过程中,
令![]() 与
与![]() 相交于两点
相交于两点![]() 和
和![]() (
(![]() 在左),
在左),
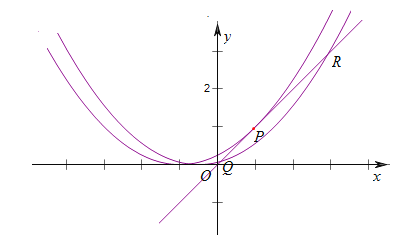
由图可知,当点![]() 与
与![]() 重合时,点
重合时,点![]() 的横坐标即为
的横坐标即为![]() 的最大值.
的最大值.
此时![]() ,得
,得![]() 或-4,∴
或-4,∴![]() .
.
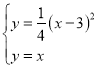 消去
消去![]() 得:
得:![]() ,解得
,解得![]() 或9,
或9,
∴![]() 的最大值为9.
的最大值为9.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目