题目内容
 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
详见解析.
试题分析:采用分析证明的方法,根据结论
 ,可得
,可得 ;再利用A,B,C成等差数列,可得
;再利用A,B,C成等差数列,可得 ,利用余弦定理可得
,利用余弦定理可得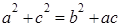 成立,代入求解即可证明结论.
成立,代入求解即可证明结论.证明:要证原式成立,只要证
 (3分)
(3分)即证
 ,即
,即 (7分)
(7分)而三个内角
 成等差数列,
成等差数列, 上式成立(11分)
上式成立(11分)故原式大成立(12分).

练习册系列答案
相关题目
题目内容
 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
 ,可得
,可得 ;再利用A,B,C成等差数列,可得
;再利用A,B,C成等差数列,可得 ,利用余弦定理可得
,利用余弦定理可得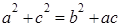 成立,代入求解即可证明结论.
成立,代入求解即可证明结论. (3分)
(3分) ,即
,即 (7分)
(7分) 成等差数列,
成等差数列, 上式成立(11分)
上式成立(11分)