题目内容
在无穷数列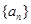 中,
中,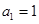 ,对于任意
,对于任意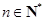 ,都有
,都有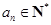 ,
,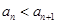 . 设
. 设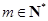 , 记使得
, 记使得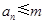 成立的
成立的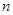 的最大值为
的最大值为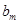 .
.
(1)设数列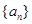 为1,3,5,7,
为1,3,5,7,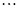 ,写出
,写出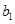 ,
,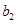 ,
,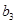 的值;
的值;
(2)若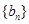 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列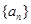 ;
;
(3)设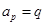 ,
,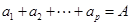 ,求
,求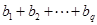 的值.(用
的值.(用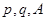 表示)
表示)
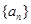 中,
中,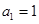 ,对于任意
,对于任意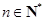 ,都有
,都有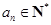 ,
,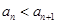 . 设
. 设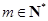 , 记使得
, 记使得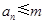 成立的
成立的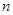 的最大值为
的最大值为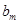 .
.(1)设数列
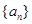 为1,3,5,7,
为1,3,5,7,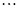 ,写出
,写出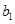 ,
,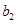 ,
,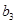 的值;
的值;(2)若
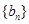 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列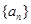 ;
;(3)设
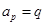 ,
,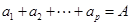 ,求
,求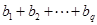 的值.(用
的值.(用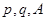 表示)
表示)(1) ,
, ,
,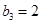 ;(2)
;(2) ;(3)
;(3) .
.
 ,
, ,
,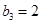 ;(2)
;(2) ;(3)
;(3) .
.试题分析:(1)根据使得
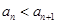 成立的
成立的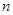 的最大值为
的最大值为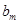 ,
, ,则
,则 ,
, ,则
,则 ,
, ,则
,则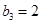 ,这样就写出
,这样就写出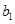 ,
,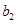 ,
,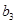 的值;(2)若
的值;(2)若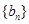 为等差数列,先判断
为等差数列,先判断 ,再证明
,再证明 ,即可求出所有可能的数列
,即可求出所有可能的数列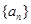 ;(3)确定
;(3)确定 ,
, ,依此类推,发现规律,得出
,依此类推,发现规律,得出 ,从而求出
,从而求出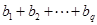 的值.
的值.(1)
 ,
, ,
,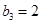 . 3分
. 3分(2)由题意,得
 ,
,结合条件
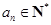 ,得
,得 . 4分
. 4分又因为使得
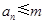 成立的
成立的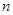 的最大值为
的最大值为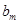 ,使得
,使得 成立的
成立的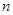 的最大值为
的最大值为 ,
,所以
 ,
, . 5分
. 5分设
 ,则
,则 .
.假设
 ,即
,即 ,
,则当
 时,
时, ;当
;当 时,
时, .
.所以
 ,
, .
.因为
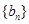 为等差数列,
为等差数列,所以公差
 ,
,所以
 ,其中
,其中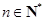 .
.这与
 矛盾,
矛盾,所以
 . 6分
. 6分又因为
 ,
,所以
 ,
,由
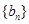 为等差数列,得
为等差数列,得 ,其中
,其中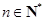 . 7分
. 7分因为使得
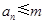 成立的
成立的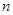 的最大值为
的最大值为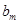 ,
,所以
 ,
,由
 ,得
,得 . 8分
. 8分(3)设
 ,
,因为
 ,
,所以
 ,且
,且 ,
,所以数列
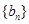 中等于1的项有
中等于1的项有 个,即
个,即 个; 9分
个; 9分设
 ,
,则
 , 且
, 且 ,
,所以数列
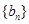 中等于2的项有
中等于2的项有 个,即
个,即 个; 10分
个; 10分以此类推,数列
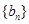 中等于
中等于 的项有
的项有 个. 11分
个. 11分所以


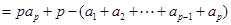
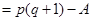 .
.即
 . 13分
. 13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三个内角
的三个内角 成等差数列,求证:
成等差数列,求证:
 的首项为
的首项为 ,公差为
,公差为 ,其前n项和为
,其前n项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则数列
对称,则数列 的前10项和=( )
的前10项和=( )

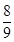
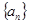 的前
的前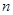 项和为
项和为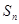 ,
,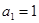 ,且
,且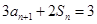 (
(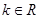 ,使得
,使得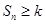 恒成立?若存在,求是实数
恒成立?若存在,求是实数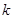 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由. 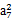 +2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )
+2a11=0,数列{bn}是等比数列,且b7=a7,则b6b8=( )
 中,
中,  , 那么它的公差是( )
, 那么它的公差是( )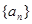 中,
中,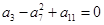 ,数列
,数列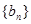 是等比数列,且
是等比数列,且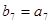 ,则
,则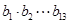 等于 .
等于 .