题目内容
20.已知双曲线C1、C2的顶点重合,C1的方程为$\frac{{x}^{2}}{4}$-y2=1,若C2的一条渐近线的斜率是C1的一条渐近线的斜率的2倍,则C2的方程为$\frac{x^2}{4}-\frac{y^2}{4}=1$.分析 求出C1的一条渐近线的斜率,可得C2的一条渐近线的斜率,利用双曲线C1、C2的顶点重合,可得C2的方程.
解答 解:C1的方程为$\frac{{x}^{2}}{4}$-y2=1,一条渐近线的方程为y=$\frac{x}{2}$,
因为C2的一条渐近线的斜率是C1的一条渐近线的斜率的2倍,
所以C2的一条渐近线的方程为y=x,
因为双曲线C1、C2的顶点重合,
所以C2的方程为$\frac{x^2}{4}-\frac{y^2}{4}=1$.
故答案为:$\frac{x^2}{4}-\frac{y^2}{4}=1$.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.已知0<m<1,设a=logm(m2+1),b=logm(m+1),c=logm(2m),则a,b,c的大小关系是( )
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | b>a>c |
11.设集合S=$\left\{{x|\frac{1}{2}<{2^x}<8}\right\}$,T={x|x<a或x>a+2},S∪T=R,则a的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
2.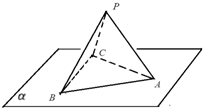 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )| A. | [$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$] | B. | [$\frac{54\sqrt{13}}{13}$,9$\sqrt{3}$] | C. | [$\frac{48\sqrt{13}}{13}$,12$\sqrt{3}$] | D. | [$\frac{48\sqrt{13}}{13}$,3$\sqrt{39}$] |