题目内容
19.已知函数f(x)=ax3+bx2+cx+d为奇函数,且在x=-1处取得极大值2.(1)求f(x)的解析式.
(2)若f(x)+(m+2)x≤x2(ex-1)对于任意的x∈[0,+∞)恒成立,求实数m的取值范围.
分析 (1)由f(x)=ax3+bx2+cx+d为奇函数知b=d=0,再由f(x)在x=-1处取得极大值2知$\left\{\begin{array}{l}{f′(-1)=3a+c=0}\\{f(-1)=-a-c=2}\end{array}\right.$,从而解得;
(2)化简f(x)+(m+2)x≤x2(ex-1)为(m+2)x≤x2(ex-1)-x3+3x,从而分x=0与x≠0讨论,从而化恒成立问题为最值问题即可.
解答 解:(1)∵f(x)=ax3+bx2+cx+d为奇函数,
∴b=d=0,
∴f(x)=ax3+cx,f′(x)=3ax2+c;
又∵f(x)在x=-1处取得极大值2,
∴$\left\{\begin{array}{l}{f′(-1)=3a+c=0}\\{f(-1)=-a-c=2}\end{array}\right.$,
解得,a=1,c=-3;
故f(x)解析式为f(x)=x3-3x;
(2)∵f(x)+(m+2)x≤x2(ex-1),
∴x3-3x+(m+2)x≤x2(ex-1),
即(m+2)x≤x2(ex-1)-x3+3x,
当x=0时,m∈R;
当x>0时,
m+2≤xex-x-x2+3,
即m≤x(ex-x-1)+1,
令h(x)=ex-x-1,h′(x)=ex-1>0,
∴h(x)在(0,+∞)上单调递增,
故h(x)>h(0)=0;
∴x(ex-x-1)+1>1;
∴m≤1;
∴实数m的取值范围为(-∞,1].
点评 本题考查了导数的综合应用及恒成立问题与最值问题,同时考查了分类讨论的思想应用,属于难题.

练习册系列答案
相关题目
19.已知平面向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则y=( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |
14.已知平面α,β,直线m,n,下列命题中不正确的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |
9.设函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |
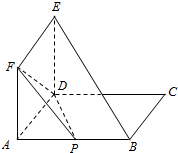 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.