题目内容
5.若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为$\frac{π}{3}$.分析 设圆锥的底面半径为r,高为h,母线长为l,由已知中圆锥的侧面积与过轴的截面面积之比为2π,可得l=2h,进而可得其母线与轴的夹角的余弦值,进而得到答案.
解答 解:设圆锥的底面半径为r,高为h,母线长为l,
则圆锥的侧面积为:πrl,过轴的截面面积为:rh,
∵圆锥的侧面积与过轴的截面面积之比为2π,
∴l=2h,
设母线与轴的夹角为θ,
则cosθ=$\frac{h}{l}$=$\frac{1}{2}$,
故θ=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查的知识点是旋转体,其中根据已知求出圆锥的母线与轴的夹角的余弦值,是解答的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.已知偶函数f(x),当x∈[0,2)时,f(x)=2sinx,当x∈[2,+∞)时,f(x)=log2x,则$f({-\frac{π}{3}})+f(4)$=( )
| A. | $\sqrt{3}+2$ | B. | 1 | C. | 3 | D. | $-\sqrt{3}+2$ |
10.设 Pn(xn,yn)是直线2x-y=$\frac{n}{n+1}$(n∈N*)与圆x2+y2=2在第一象限的交点,则极限$\lim_{n→∞}\frac{{{y_n}-1}}{{{x_n}-1}}$=( )
| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 2 |
5.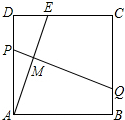 在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
 在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )| A. | 5:12 | B. | 5:13 | C. | 5:19 | D. | 5:21 |
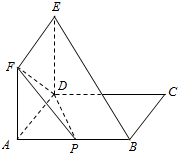 如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.
如图所示:矩形ABCD与正方形ADEF所在的平面互相垂直,AB=2AD=4,点P为AB的中点.