题目内容
2. 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )| A. | [$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$] | B. | [$\frac{54\sqrt{13}}{13}$,9$\sqrt{3}$] | C. | [$\frac{48\sqrt{13}}{13}$,12$\sqrt{3}$] | D. | [$\frac{48\sqrt{13}}{13}$,3$\sqrt{39}$] |
分析 如图所示,面PBC⊥面α,正投影图的面积最小,求出正投影图的面积最大值,即可得出结论.
解答 解:如图1所示,当平面PBC⊥平面α时正三棱锥P-ABC在α上的正投影图的面积最小,
此时PP′=6,P′D=$\sqrt{3}$,PD=$\sqrt{39}$,
所以cos∠PDP′=$\frac{\sqrt{3}}{\sqrt{39}}$,
当面PBC⊥面α,cos∠ADA′=$\frac{6}{\sqrt{39}}$,
所以A′D=3$\sqrt{3}$×$\frac{6}{\sqrt{39}}$=$\frac{18}{\sqrt{13}}$,
所以S△A′BC=$\frac{1}{2}×6×$$\frac{18}{\sqrt{13}}$=$\frac{54\sqrt{13}}{13}$.
如图2所示,当平面ABC在平面α内时正三棱锥P-ABC在α上的正投影图的面积最大,
此时投影图的面积=S△ABC+S△P′BC,
因为S△ABC=$\frac{\sqrt{3}}{4}×{6}^{2}$=9$\sqrt{3}$,S△P′BC=$\frac{1}{2}$P′D×BC=$\frac{1}{2}$×$\sqrt{3}$×6=3$\sqrt{3}$,
∴投影图的面积=S△ABC+S△P′BC=9$\sqrt{3}$+3$\sqrt{3}$=12$\sqrt{3}$
所以在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是[$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$].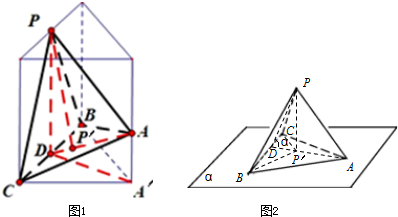
故选:A.
点评 本题考查图形的旋转,考查面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
14.已知平面α,β,直线m,n,下列命题中不正确的是( )
| A. | 若m⊥α,m⊥β,则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m⊥α,m?β,则α⊥β | D. | 若m∥α,α∩β=n,则m∥n |