题目内容
20.在平面直角坐标系xOy中,已知点A(-2,2)、B(2,6),一条直线l过点(0,m),且与单位圆x2+y2=1恒相切,若有且只有两个点P满足:①$\overrightarrow{PA}$$•\overrightarrow{PB}$=-4
②点P到直线l的距离为1
则实数m的取值范围是(-∞,-2)∪(1,+∞).
分析 设直线l:y=kx+m,由l与单位圆x2+y2=1恒相切,由相切的条件可得k,m的关系式,设P的坐标(a,b),由向量的数量积的坐标表示可得P在圆心为(0,4),半径为2的圆上,再由点到直线的距离公式,设出直线y=kx+t,求得t,m的关系式,由直线y=kx+t与在圆心为(0,4),半径为2的圆相交,解不等式即可得到m的范围.
解答 解:设直线l:y=kx+m,由l与单位圆x2+y2=1恒相切,
可得$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,即1+k2=m2,
设P(a,b),则$\overrightarrow{PA}$=(-2-a,2-b),$\overrightarrow{PB}$=(2-a,6-b),
由①可得(-2-a)(2-a)+(2-b)(6-b)=-4,
化简可得a2+b2-8b+12=0,
即有P在圆心为(0,4),半径为2的圆上,
设到直线l的距离为1的直线为y=kx+t,
可得$\frac{|t-m|}{\sqrt{1+{k}^{2}}}$=1,
将1+k2=m2,代入上式,可得|t-m|=|m|,
解得t=0或2m.
当t=0时,由题意可得直线y=kx与圆心为(0,4),半径为2的圆相交,
即有1<$\frac{4}{\sqrt{1+{k}^{2}}}$<2,即为|m|>2,解得m>2或m<-2;
当t=2m时,由题意可得直线y=kx+2m与圆心为(0,4),半径为2的圆相交,
即有$\frac{|2m-4|}{\sqrt{1+{k}^{2}}}$<2,即为|m|>|m-2|,解得m>1.
综上可得m>1或m<-2.
故答案为:(-∞,-2)∪(1,+∞).
点评 本题考查直线和圆的位置关系:相交和相切,同时考查向量的数量积的坐标表示,考查运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案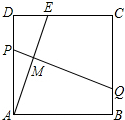 在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )
在祖国60年国庆庆典晚会上,需制作表演道具,如图.将一块边长为12的正方形纸ABCD的顶点A折叠至边上的点E,使DE=5,折痕为PQ,则线段PM和MQ的比是( )| A. | 5:12 | B. | 5:13 | C. | 5:19 | D. | 5:21 |
| A. | 奇函数 | B. | 偶函数 | C. | 非奇非偶函数 | D. | 既奇又偶函数 |