题目内容
1.已知函数f(x)=mx|x-1|-|x|+1,则关于函数y=f(x)的零点情况,下列说法中正确的是( )| A. | 当-1≤m≤-3+2$\sqrt{2}$时,函数y=f(x)有且仅有一个零点 | |
| B. | 当m=-3+2$\sqrt{2}$或m≤-1或m≥1或m=0时,函数y=f(x)有两个零点 | |
| C. | 当-3+2$\sqrt{2}$<m<0或0<m<1时,y=f(x)有三个零点 | |
| D. | 函数y=f(x)最多可能有四个零点 |
分析 函数f(x)=mx|x-1|-|x|+1的零点情况即函数y1=mx|x-1|与函数y2=|x|-1的交点个数,作函数的图象求解即可.
解答 解:记y1=mx|x-1|,y2=|x|-1;
函数f(x)=mx|x-1|-|x|+1的零点情况即函数y1=mx|x-1|与函数y2=|x|-1的交点个数,
作出函数y1=mx|x-1|与函数y2=|x|-1的图象如下,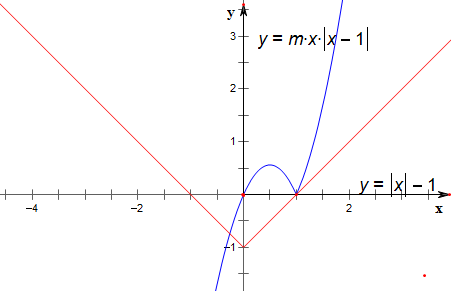
①当m≥1时,两函数图象有2个交点;
②当0<m<1时,两函数图象有3个交点;
③当m=0时,两函数图象有2个交点;
④当-3+2$\sqrt{2}$<m<0时,两函数图象有3个交点;
⑤当m=-3+2$\sqrt{2}$时,两函数图象有2个交点;
⑥当-1≤m<-3+2$\sqrt{2}$时,两函数图象有1个交点;
⑦当m<-1时,两函数图象有2个交点;
综上可得,当m=-3+2$\sqrt{2}$或m≤-1或m≥1或m=0时,函数y=f(x)有两个零点;
故选:C.
点评 本题考查了函数的零点与函数的交点的关系应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列命题中,正确的是( )
| A. | 如果直线a∥b,那么a平行于经过b的任何平面 | |
| B. | 如果直线a,b和平面α满足a∥α,b∥α,那么a∥b | |
| C. | 如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
9.复数z满足(-1+i)z=(1+i)2,其中i为虚数单位,则|z|=( )
| A. | 2 | B. | -2 | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
6.已知x,y∈(-∞,0),且x+y=-1,则xy+$\frac{1}{xy}$有( )
| A. | 最大值$\frac{17}{4}$ | B. | 最小值$\frac{17}{4}$ | C. | 最小值-$\frac{17}{4}$ | D. | 最大值-$\frac{17}{4}$ |
11.“θ≠$\frac{π}{3}$”是“tanθ≠$\sqrt{3}$”的( )
| A. | 必要但非充分条件 | B. | 充分但非必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
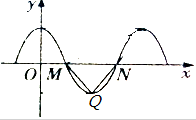 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.