题目内容
11.下列命题中,正确的是( )| A. | 如果直线a∥b,那么a平行于经过b的任何平面 | |
| B. | 如果直线a,b和平面α满足a∥α,b∥α,那么a∥b | |
| C. | 如果平面α⊥平面β,那么平面α内的所有直线都垂直于平面β | |
| D. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
分析 由线面平行的判定定理,可以判断A的真假;由线面平行的定义判定定理以及性质定理的应用即可判断B;C结合实物举反例即可;D用反证法及面面垂直的判定定理即可判断.
解答 解:A选项:如果a,b是两条直线,且a∥b,那么a平行于经过b但不经过a的任何平面,故A错误;
B选项:a可以与直线b平行,异面,相交.故此命题错误;
C选项:举反例:教室内侧墙面与地面垂直,而侧墙面内有很多直线是不垂直与地面的.故此命题错误;
D选项:假若平面α内存在直线垂直于平面β,根据面面垂直的判定定理可知两平面垂直.故此命题成立;
故选:D.
点评 本题考查的是空间中直线与平面之间的位置关系,在解答的过程当中充分体现了面面垂直、线面垂直、线面平行的定义判定定理以及性质定理的应用,属于基本知识的考查.

练习册系列答案
相关题目
5.为了了解城市人均GDP与人均日产生活垃圾量之间的相关关系,国家统计局与卫生管理局随机抽查了6个城市,具体数据如表
(1)计算这6个城市人均日产生活垃圾量的平均值(单位:千克);
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
| 城市 | 天津 | 重庆 | 广州 | 深圳 | 武汉 | 西安 |
| 人均GDP(万美元)x | 1.64 | 0.69 | 1.93 | 2.22 | 1.43 | 0.92 |
| 人均日产生活垃圾量(千克)y | 0.64 | 0.51 | 1.05 | 1.15 | 0.99 | 0.76 |
(2)求出x与y之间的线性回归方程;
(提供下列参考数据:$\sum_{i=1}^6{x_i}=8.82$,$\sum_{i=1}^6{x_i}{y_i}=8.1$,$\sum_{i=1}^6{x_i}^2=14.7$)
(3)如果某城市的人均GDP达到了3万美元,预测该城市的人均日产生活垃圾量为多少千克?
6.已知f′(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,xf′(x)+f(x)>0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
6.椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
3.已知a=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,b=log5$\frac{1}{3}$,c=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
1.已知函数f(x)=mx|x-1|-|x|+1,则关于函数y=f(x)的零点情况,下列说法中正确的是( )
| A. | 当-1≤m≤-3+2$\sqrt{2}$时,函数y=f(x)有且仅有一个零点 | |
| B. | 当m=-3+2$\sqrt{2}$或m≤-1或m≥1或m=0时,函数y=f(x)有两个零点 | |
| C. | 当-3+2$\sqrt{2}$<m<0或0<m<1时,y=f(x)有三个零点 | |
| D. | 函数y=f(x)最多可能有四个零点 |
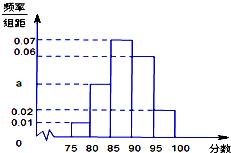 某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直
某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直