题目内容
9.复数z满足(-1+i)z=(1+i)2,其中i为虚数单位,则|z|=( )| A. | 2 | B. | -2 | C. | √2 | D. | -√2 |
分析 直接利用复数的模的求解方法,化简求解即可.
解答 解:复数z满足(-1+i)z=(1+i)2,其中i为虚数单位,
可得|-1+i||z|=|(1+i)2|,
√2|z|=√2•√2,
|z|=√2.
故选:C.
点评 本题考查复数的模的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知在三棱锥P-ABC中,PA=4,AC=2√7,PB=BC=2√3,PA⊥平面PBC,则三棱锥P-ABC的内切球的表面积为( )
| A. | 32π | B. | 3π | C. | 94π | D. | 4π |
4.若数列{an}中,a1=1,an+1=-12an(n∈N*),则an=( )
| A. | (-12)n-1 | B. | -(12)n-1 | C. | (-12)n | D. | -(12)n |
1.已知函数f(x)=mx|x-1|-|x|+1,则关于函数y=f(x)的零点情况,下列说法中正确的是( )
| A. | 当-1≤m≤-3+2√2时,函数y=f(x)有且仅有一个零点 | |
| B. | 当m=-3+2√2或m≤-1或m≥1或m=0时,函数y=f(x)有两个零点 | |
| C. | 当-3+2√2<m<0或0<m<1时,y=f(x)有三个零点 | |
| D. | 函数y=f(x)最多可能有四个零点 |
18.设双曲线方程mx2-ny2=1(mn≠0),则“离心率e=√2”是“m=n”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |

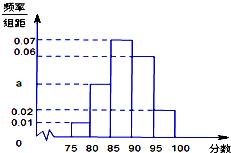 某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直
某地区有800名学员参加交通法规考试,考试成绩的 频率分 布直