题目内容
12. 函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.
函数f(x)=Acosωx(A>0,ω>0)部分图象如图所示,其中M,N(12,0),Q分别是函数图象在y轴右侧第一,二个零点,第一个最低点,且△MQN是等边三角形.求函数f(x)的解析式.
分析 求出函数的周期,利用三角函数的图象和性质即可得到结论.
解答 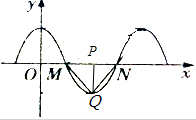 解:过Q作x轴的垂线交MN于P,
解:过Q作x轴的垂线交MN于P,
∵$\frac{3T}{4}=12$,可得函数的周期T=$\frac{2π}{ω}$=16,解得:ω=$\frac{π}{8}$,
∴M(4,0),MN=8,MP=4,
∵∠PPQ=90°,∠PMQ=60°
∴则PQ=MPtan∠PMQ=4×tan60°=4$\sqrt{3}$,可得Q(8,-4$\sqrt{3}$),
∴由-4$\sqrt{3}$=Acosπ可得:A=4$\sqrt{3}$
故函数f(x)的解析式为:f(x)=4$\sqrt{3}$cos$\frac{π}{8}$x.
点评 本题主要考查三角函数的图象和性质,求出函数的周期,利用直角三角形的性质是解决本题的关键,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知f′(x)是奇函数f(x)的导函数,f(-1)=0,当x>0时,xf′(x)+f(x)>0,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
3.已知a=($\frac{1}{5}$)${\;}^{-\frac{1}{2}}$,b=log5$\frac{1}{3}$,c=log${\;}_{\frac{1}{5}}$$\frac{1}{3}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
7.已知扇形圆心角的弧度数为2,半径为3cm,则扇形的面积为( )
| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
17.已知在三棱锥P-ABC中,PA=4,AC=2$\sqrt{7}$,PB=BC=2$\sqrt{3}$,PA⊥平面PBC,则三棱锥P-ABC的内切球的表面积为( )
| A. | $\frac{3}{2}$π | B. | 3π | C. | $\frac{9}{4}$π | D. | 4π |
4.若数列{an}中,a1=1,an+1=-$\frac{1}{2}$an(n∈N*),则an=( )
| A. | (-$\frac{1}{2}$)n-1 | B. | -($\frac{1}{2}$)n-1 | C. | (-$\frac{1}{2}$)n | D. | -($\frac{1}{2}$)n |
1.已知函数f(x)=mx|x-1|-|x|+1,则关于函数y=f(x)的零点情况,下列说法中正确的是( )
| A. | 当-1≤m≤-3+2$\sqrt{2}$时,函数y=f(x)有且仅有一个零点 | |
| B. | 当m=-3+2$\sqrt{2}$或m≤-1或m≥1或m=0时,函数y=f(x)有两个零点 | |
| C. | 当-3+2$\sqrt{2}$<m<0或0<m<1时,y=f(x)有三个零点 | |
| D. | 函数y=f(x)最多可能有四个零点 |