题目内容
6．
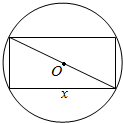如图，截面半径为20cm的圆形木料，如果矩形的边长为x（cm），面积为y（cm2），求出y与x的函数关系式．
分析 首先根据矩形的一边长为xcm，表示出另外一边的长度，然后直接列出y关于x的函数．
解答 解：∵矩形的一边长为xcm，
∴矩形的另一边长为$\sqrt{1600-{x}^{2}}$cm，
∴$y=x\sqrt{1600-{x}^{2}}$，因为直径为40cm，
所以0＜x＜40
故答案为：$y=x\sqrt{1600-{x}^{2}}$（0＜x＜40）．
点评 本题考查函数模型的选择与应用，通过对实际问题的分析，抽象出数学模型，把y表示为x的函数，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
14．若方程$\frac{x^2}{2m}$+$\frac{y^2}{1-m}$=1表示双曲线，则实数m的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，1） | C． | （0，1） | D． | （-∞，0）∪（1，+∞） |
11．上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关，随机抽取了55名市民，得到数据如下表：
（1）判断是否有99.5%的把握认为喜欢观看体育节目与性别有关？
（2）用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求男市民人数ξ的分布列和期望．
下面的临界值表参考：
| 喜欢 | 不喜欢 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
（2）用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查，将这6位市民作为一个样本，从中任选2人，求男市民人数ξ的分布列和期望．
下面的临界值表参考：
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18．已知函数f（x）=lg（x2-2ax+2），若对任意的x1，x2∈（-∞，1]且x1≠x2，均有[f（x1）-f（x2）]（ x1-x2 ）＜0成立，则实数a的取值范围是（ ）
| A． | （1，+∞） | B． | [1，+∞） | C． | （1，$\frac{3}{2}$） | D． | [1，$\frac{3}{2}$] |