题目内容
15.计算:$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$10.分析 利用二阶矩阵乘法法则进行求解.
解答 解:$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$10=$(\begin{array}{l}{1}&{2}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$8=$(\begin{array}{l}{1}&{3}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$7=$(\begin{array}{l}{1}&{4}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$6
=$(\begin{array}{l}{1}&{5}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$5=$(\begin{array}{l}{1}&{6}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$4=$(\begin{array}{l}{1}&{7}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$3
=$(\begin{array}{l}{1}&{8}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$2=$(\begin{array}{l}{1}&{9}\\{0}&{1}\end{array})$$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$=$(\begin{array}{l}{1}&{10}\\{0}&{1}\end{array})$.
∴$(\begin{array}{l}{1}&{1}\\{0}&{1}\end{array})$10=$(\begin{array}{l}{1}&{10}\\{0}&{1}\end{array})$.
点评 本题考查二阶矩阵的乘法运算,是基础题,解题时要注意二阶矩阵乘法法则的合理运用.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案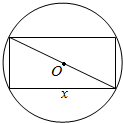 如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.
如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.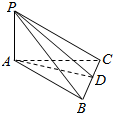 如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.
如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.