题目内容
14．若方程$\frac{x^2}{2m}$+$\frac{y^2}{1-m}$=1表示双曲线，则实数m的取值范围是（ ）| A． | （-∞，0） | B． | （-∞，1） | C． | （0，1） | D． | （-∞，0）∪（1，+∞） |
分析 根据双曲线的标准方程，列出不等式2m（1-m）＜0，求出实数m的取值范围即可．
解答 解：方程$\frac{x^2}{2m}$+$\frac{y^2}{1-m}$=1表示双曲线，
则2m（1-m）＜0，
即m（m-1）＞0；
解得m＜0或m＞1，
∴实数m的取值范围是（-∞，0）∪（1，+∞）．
故选：D．
点评 本题考查了双曲线的定义与标准方程的应用问题，是基础题目．
练习册系列答案
相关题目
2．甲、乙、丙三位学生独立地解同一道题，甲乙做对的概率分别为$\frac{1}{2}$，$\frac{1}{3}$，丙做对的概率为m，且三位学生是否做对相互独立．记ξ为这三位学生中做对该题的人数，其分布列为：
（1）求至少有一位学生做对该题的概率；
（2）求m的值；
（3）求ξ的数学期望．
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | a | b | $\frac{1}{24}$ |
（2）求m的值；
（3）求ξ的数学期望．
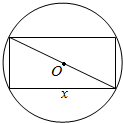如图，截面半径为20cm的圆形木料，如果矩形的边长为x（cm），面积为y（cm2），求出y与x的函数关系式．
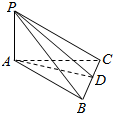如图所示，已知PA⊥面ABC，S△PBC=S，S△ABC=S′，二面角P-BC-A的平面角为θ，求证S•cosθ=S′．