题目内容
18.已知函数f(x)=lg(x2-2ax+2),若对任意的x1,x2∈(-∞,1]且x1≠x2,均有[f(x1)-f(x2)]( x1-x2 )<0成立,则实数a的取值范围是( )| A. | (1,+∞) | B. | [1,+∞) | C. | (1,$\frac{3}{2}$) | D. | [1,$\frac{3}{2}$] |
分析 利用题目条件可判断单调递减,
故考虑对称轴的位置,再考虑对数的限制条件u(1)>0,即可得出范围.
解答 解:∵对任意的x1,x2∈(-∞,1]且x1≠x2,均有[f(x1)-f(x2)]( x1-x2 )<0成立.
u(x)=x2-2ax+2的对称轴:x=a
∴$\left\{\begin{array}{l}{a≥1}\\{{1}^{2}-2a+2>0}\end{array}\right.$
解得1$≤a<\frac{3}{2}$.
故选:C
点评 本题考察了单调性的判断,符合函数的单调性,对数函数的定义域的限制,难度不大,特别容易出错.

练习册系列答案
相关题目
13.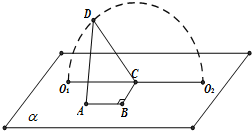 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
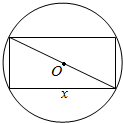 如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.
如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.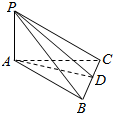 如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.
如图所示,已知PA⊥面ABC,S△PBC=S,S△ABC=S′,二面角P-BC-A的平面角为θ,求证S•cosθ=S′.