题目内容
16．解不等式：x2-2（a+1）x+1≤0．分析 由二次函数和二次不等式的关系，针对△分类讨论可得．
解答 解：当△=4（a+1）2-4＜0即-2＜a＜0时，原不等式的解集为R；
当△=4（a+1）2-4=0即a=0或a=-2时，原不等式的解集为{x|x=±1}；
当△=4（a+1）2-4＞0即a＜-2或a＞0时，原不等式的解集为{x|a+1-$\sqrt{{a}^{2}+2a}$＜x＜a+1+$\sqrt{{a}^{2}+2a}$}
点评 本题考查一元二次不等式的解集，涉及分类讨论的思想，属中档题．
练习册系列答案
相关题目
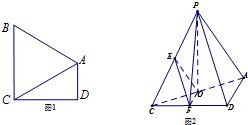如图1，在直角梯形ABCD中，AD∥BC，∠ADC=90°，BA=BC=AC=2，把△BAC沿AC折起到△PAC的位置，使得P点在平面ADC上的正投影O恰好落在线段AC上，如图2所示．点E，F分别为棱PC，CD的中点．
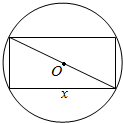如图，截面半径为20cm的圆形木料，如果矩形的边长为x（cm），面积为y（cm2），求出y与x的函数关系式．