题目内容
1.一元二次方程x2-4x+a=0有两个实根,一个比3大,一个比3小,求a的取值范围.分析 设f(x)=x2-4x+a,则由题意可得f(3)=a-3<0,由此求得a的范围.
解答 解:设f(x)=x2-4x+a,则由题意可得f(3)=a-3<0,求得a<3.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
12.函数y=log${\;}_{\frac{1}{2}}$(1-2x)的值域为( )
| A. | (-∞,+∞) | B. | (-∞,0) | C. | (0,+∞) | D. | (1,+∞) |
16.图是截去了一个角的正方体,则它的俯视图为( )
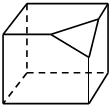

| A. | 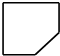 | B. | 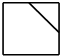 | C. | 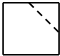 | D. | 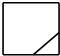 |
13.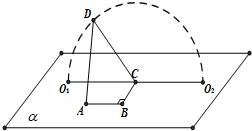 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
 如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )
如图,A、B、C,O1,O2∈平面α,AB=BC=1,∠ABC=90°,D为动点,DC=$\sqrt{3}$,且DC⊥BC.当点D从O1顺时针转动到O2的过程中,异面直线AD与BC所成角的余弦值( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
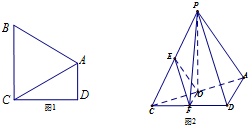 如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点.
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC=AC=2,把△BAC沿AC折起到△PAC的位置,使得P点在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E,F分别为棱PC,CD的中点. 如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.
如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.