题目内容
15.已知函数f(x)=2sin(x+$\frac{π}{2}$)sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx.(1)求f(x)的最小正周期;
(2)当α∈[0,π]时,若f(α)=1,求α的值.
分析 (1)由三角函数公式化简可得f(x)=sin(2x+$\frac{π}{3}$),由周期公式可得;
(2)由题意可得sin(2α+$\frac{π}{3}$)=1,可得2α+$\frac{π}{3}$=2kπ+$\frac{π}{2}$,k∈Z,结合α的范围可得.
解答 解:(1)由三角函数公式化简可得:
f(x)=2sin(x+$\frac{π}{2}$)sin(x+$\frac{π}{3}$)-$\sqrt{3}$sin2x+sinxcosx
=2cosx($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)-$\sqrt{3}$sin2x+sinxcosx
=sinxcosx+$\sqrt{3}$cos2x-$\sqrt{3}$sin2x+sinxcosx
=2sinxcosx+$\sqrt{3}$(cos2x-sin2x)
=sin2x+$\sqrt{3}$cos2x=sin(2x+$\frac{π}{3}$),
∴f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)∵f(α)=sin(2α+$\frac{π}{3}$)=1,
∴2α+$\frac{π}{3}$=2kπ+$\frac{π}{2}$,∴α=kπ+$\frac{π}{12}$,k∈Z,
∵α∈[0,π],∴α=$\frac{π}{12}$.
点评 本题考查三角函数恒等变换,涉及三角函数的周期性,属基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5.已知全集U={0,1,2,3,4},A={1,2,3},B={0,2}则A∩(∁UB)等于( )
| A. | { 1,2,3,4} | B. | { 0,1,2,3 } | C. | { 1,2 } | D. | { 1,3 } |
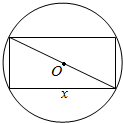 如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.
如图,截面半径为20cm的圆形木料,如果矩形的边长为x(cm),面积为y(cm2),求出y与x的函数关系式.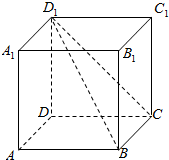
 如图,已知三棱台ABC-A′B′C′.
如图,已知三棱台ABC-A′B′C′.