题目内容
已知直线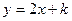 被抛物线
被抛物线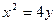 截得的
截得的
弦长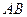 为20,
为20,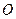 为坐标原点.
为坐标原点.
(1)求实数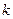 的值;
的值;
(2)问点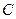 位于抛物线弧
位于抛物线弧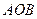 上何处时,△
上何处时,△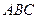 面积最大?
面积最大?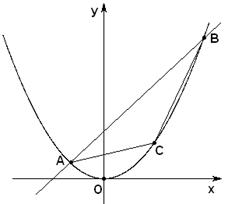
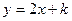 被抛物线
被抛物线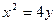 截得的
截得的弦长
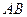 为20,
为20,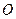 为坐标原点.
为坐标原点.(1)求实数
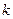 的值;
的值;(2)问点
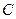 位于抛物线弧
位于抛物线弧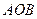 上何处时,△
上何处时,△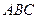 面积最大?
面积最大?
(1)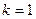 (2)
(2) 位于(4,4)点处
位于(4,4)点处
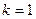 (2)
(2) 位于(4,4)点处
位于(4,4)点处【解题思路】用“韦达定理”求弦长;考虑△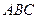 面积的最大值取得的条件
面积的最大值取得的条件
1)将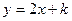 代入
代入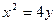 得
得 ,
,
由△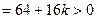 可知
可知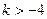 ,
,
另一方面,弦长AB ,解得
,解得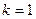 ;
;
(2)当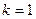 时,直线为
时,直线为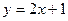 ,要使得内接△ABC面积最大,
,要使得内接△ABC面积最大,
则只须使得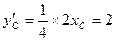 ,
,
即 ,即
,即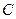 位于(4,4)点处.
位于(4,4)点处.
【名师指引】用“韦达定理”不要忘记用判别式确定范围
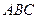 面积的最大值取得的条件
面积的最大值取得的条件1)将
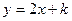 代入
代入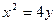 得
得 ,
,由△
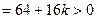 可知
可知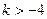 ,
,另一方面,弦长AB
 ,解得
,解得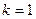 ;
;(2)当
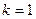 时,直线为
时,直线为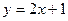 ,要使得内接△ABC面积最大,
,要使得内接△ABC面积最大,则只须使得
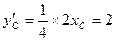 ,
,即
 ,即
,即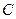 位于(4,4)点处.
位于(4,4)点处.【名师指引】用“韦达定理”不要忘记用判别式确定范围

练习册系列答案
相关题目
 轴,抛物线上一点
轴,抛物线上一点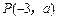 到焦点的距离为5,求抛物线的标准方程.
到焦点的距离为5,求抛物线的标准方程. 与点
与点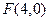 的距离比它到直线
的距离比它到直线 的距离大
的距离大 ,则点
,则点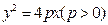 的准线与
的准线与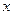 轴的交点为
轴的交点为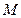 ,过点
,过点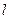 交抛物线于
交抛物线于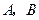 两点.若直线
两点.若直线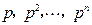 时,线段
时,线段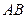 的垂直平分线与对称轴的交点依次为
的垂直平分线与对称轴的交点依次为 ,当
,当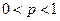 时,求
时,求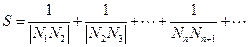 的值.
的值. 所得的弦长为
所得的弦长为 。
。 的过焦点的弦为
的过焦点的弦为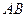 ,且
,且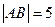 ,又
,又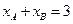 ,则
,则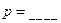
 过抛物线
过抛物线 的焦点,并且与
的焦点,并且与 轴垂直,若
轴垂直,若 ( )
( )
