题目内容
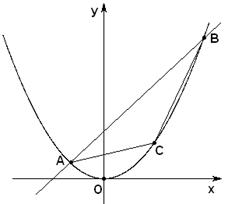
过抛物线y2=4x的顶点O作两条互相垂直的直线分别交抛物线于A、B两点,则线段AB的中点P(x,y)的轨迹方程是( )
A.y2="-2x-8 " B.y2=2x-8
C.y2="2x+8 " D.y2=-2x+8
A.y2="-2x-8 " B.y2=2x-8
C.y2="2x+8 " D.y2=-2x+8
C
设OA:y=kx,代入y2=4x得k2x2=4x,解得A(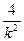 ,
,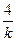 ).
).
∵OB⊥OA,则OB:y=- x,
x,
用- 代替A点坐标中的k得B(4k2,-4k).
代替A点坐标中的k得B(4k2,-4k).
又AB中点P(x,y),
∴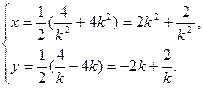
消去参数k得y2-2x-8=0.
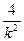 ,
,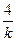 ).
).∵OB⊥OA,则OB:y=-
 x,
x,用-
 代替A点坐标中的k得B(4k2,-4k).
代替A点坐标中的k得B(4k2,-4k).又AB中点P(x,y),
∴
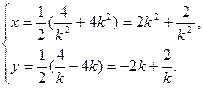
消去参数k得y2-2x-8=0.

练习册系列答案
相关题目
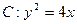 ,直线
,直线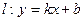 与C交于A,B两点,O为坐标原点。
与C交于A,B两点,O为坐标原点。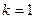 ,且直线
,且直线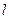 过抛物线C的焦点时,求
过抛物线C的焦点时,求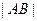 的值;
的值;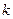 ,
,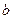 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线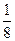
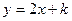 被抛物线
被抛物线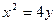 截得的
截得的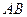 为20,
为20,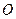 为坐标原点.
为坐标原点.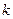 的值;
的值;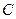 位于抛物线弧
位于抛物线弧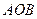 上何处时,△
上何处时,△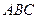 面积最大?
面积最大?