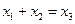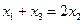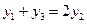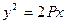题目内容
(1)顶点在原点,焦点在y轴上,抛物线上点(3,a)到焦点的距离是5;
(2)顶点在原点,焦点在x轴上的抛物线截直线
 所得的弦长为
所得的弦长为 。
。解:(1)

由(2)得
解得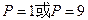
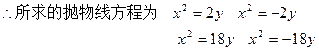
(2)设所求的抛物线方程为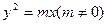



由(2)得

解得
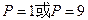
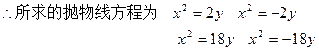
(2)设所求的抛物线方程为
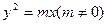

(1)由题设抛物线焦点在y轴上,但开口方向并不明确,仍有两种情况:
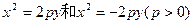 其焦点分别为:
其焦点分别为: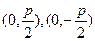 ,准线方程分别为
,准线方程分别为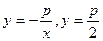 由抛物线定义得到
由抛物线定义得到 ,再由点(3,a)在抛物线上得到p,a的另一方程,消去a求得P .
,再由点(3,a)在抛物线上得到p,a的另一方程,消去a求得P .
(2)由于焦点在x轴上,但不明确抛物线的开口方向,故而可设抛物线方程: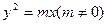 通过题设条件,求得m值,便于确定方程。
通过题设条件,求得m值,便于确定方程。
本题给出求抛物线方程的常用方法,主要是当题设只给出焦点所在的轴,而不明确开口方向时作为待定系数法的第一步:“假设方程”时的两类不同设。
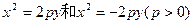 其焦点分别为:
其焦点分别为: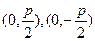 ,准线方程分别为
,准线方程分别为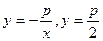 由抛物线定义得到
由抛物线定义得到 ,再由点(3,a)在抛物线上得到p,a的另一方程,消去a求得P .
,再由点(3,a)在抛物线上得到p,a的另一方程,消去a求得P .(2)由于焦点在x轴上,但不明确抛物线的开口方向,故而可设抛物线方程:
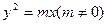 通过题设条件,求得m值,便于确定方程。
通过题设条件,求得m值,便于确定方程。本题给出求抛物线方程的常用方法,主要是当题设只给出焦点所在的轴,而不明确开口方向时作为待定系数法的第一步:“假设方程”时的两类不同设。

练习册系列答案
相关题目
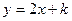 被抛物线
被抛物线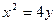 截得的
截得的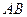 为20,
为20,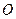 为坐标原点.
为坐标原点.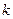 的值;
的值;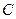 位于抛物线弧
位于抛物线弧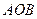 上何处时,△
上何处时,△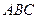 面积最大?
面积最大?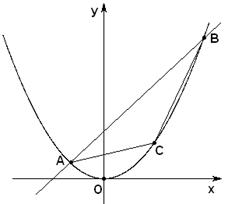
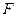 是抛物线
是抛物线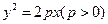 的焦点,过
的焦点,过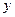 轴上的动点
轴上的动点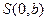 作直线
作直线 的垂线
的垂线 .
.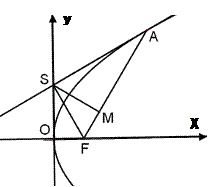
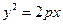 相切;
相切;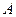 ,过点
,过点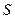 作直线
作直线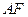 的垂线,垂足为
的垂线,垂足为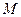 ,求线段
,求线段 的长度以及动点
的长度以及动点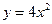 上求一点,使这点到直线
上求一点,使这点到直线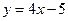 的距离最短。
的距离最短。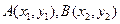 两点在抛物线
两点在抛物线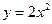 上,
上,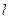 是
是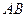 的垂直平分线,(1)当且仅当
的垂直平分线,(1)当且仅当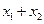 取何值时,直线
取何值时,直线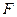 ?证明你的结论;(2)当直线
?证明你的结论;(2)当直线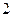 时,求
时,求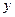 轴上的截距的取值范围。
轴上的截距的取值范围。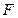 和定直线
和定直线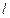 ,动圆
,动圆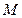 过
过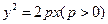 的焦点为
的焦点为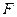 ,点
,点 ,
,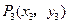 在抛物线上,且
在抛物线上,且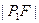 、
、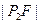 、
、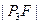 成等差数列, 则有 ( )
成等差数列, 则有 ( )