题目内容
【题目】定义一个“希望结合”(![]() )简称
)简称![]() 如下:
如下:![]() 为一个非空集合,它满足条件“若
为一个非空集合,它满足条件“若![]() ,则
,则![]() ”。试问:在集合
”。试问:在集合![]() 中,一共有多少个“希望子集合”?请说明理由。
中,一共有多少个“希望子集合”?请说明理由。
【答案】![]()
【解析】
下面用“![]() ”表示
”表示![]() 与
与![]() 的两倍关系.注意到
的两倍关系.注意到
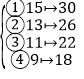
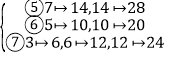
![]()
显然,![]() 是否在
是否在![]() 中不影响
中不影响![]() 成为希望子集(因为这些数不能被
成为希望子集(因为这些数不能被![]() 整除,且每个数的两倍均大于
整除,且每个数的两倍均大于![]() ),所以,这
),所以,这![]() 个数的归属方案有
个数的归属方案有![]() 种.
种.
在①中,![]() 与
与![]() 不能同时取,故有
不能同时取,故有![]() 种方案.
种方案.
同理,在②、③、④中,也各有![]() 种方案.
种方案.
下面采用递推算法.
在⑤中,若取![]() ,则不能取
,则不能取![]() ,此时,
,此时,![]() 可取亦可不取,有两种方案:若不取
可取亦可不取,有两种方案:若不取![]() ,则由①知,关于
,则由①知,关于![]() 和
和![]() ,共有
,共有![]() 种方案(
种方案(![]() 和
和![]() 的情况与①相同).因此,在⑤中共有
的情况与①相同).因此,在⑤中共有![]() 种方案.
种方案.
同理,在⑥中共有![]() 种方案.
种方案.
在⑦中,若取![]() ,则不能取
,则不能取![]() ,由①知关于
,由①知关于![]() 和
和![]() ,有
,有![]() 种方案;若不取
种方案;若不取![]() ,则由⑤知,关于
,则由⑤知,关于![]() 有
有![]() 种方案.因此,在⑦中共有
种方案.因此,在⑦中共有![]() 种方案.
种方案.
在⑧中,若取![]() ,则不能取
,则不能取![]() ,由⑤知关于
,由⑤知关于![]() ,有
,有![]() 种方案;若不取
种方案;若不取![]() ,则由⑦知关于
,则由⑦知关于![]() ,有
,有![]() 种方案.因此,在⑧中共有
种方案.因此,在⑧中共有![]() 种方案.
种方案.
再考虑到除去空集![]() (即
(即![]() 都不取),因此所求的
都不取),因此所求的![]() 的希望子集的个数为
的希望子集的个数为![]() .
.

练习册系列答案
相关题目
