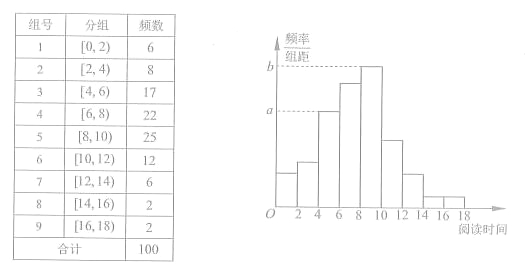
题目内容
【题目】已知函数![]() (
(![]() ,
,![]() )的图像经过点
)的图像经过点![]() ,且关于直线
,且关于直线![]() 对称,则下列结论正确的是( )
对称,则下列结论正确的是( )
A. ![]() 在
在![]() 上是减函数
上是减函数
B. 函数的最小正周期为![]()
C. ![]() 的解集是
的解集是![]() ,
,![]()
D. ![]() 的一个对称中心是
的一个对称中心是![]()
【答案】D
【解析】
由题意可得函数f(x)的解析式,由函数的单减区间可判断A,由函数周期可判断B;运用正弦函数的图象解不等式可得解集,可判断C;由对称中心解方程可判断D.
函数f(x)=2sin(ωx+![]() )(0<ω<1,|
)(0<ω<1,|![]() |
|![]() )的图象经过点(0,1),
)的图象经过点(0,1),
可得2sin![]() =1,由|
=1,由|![]() |
|![]() 即有
即有![]() ,
,
由关于直线![]() 对称,可得2sin(
对称,可得2sin(![]() ω
ω![]() )=2或-2,0<ω<1,
)=2或-2,0<ω<1,
即有![]() ω
ω![]() ,或
,或![]() ω
ω![]() ,可得ω
,可得ω![]() 或ω
或ω![]() ,又0<ω<1,
,又0<ω<1,
则f(x)=2sin(![]() x
x![]() ),
),
当x![]() 时,
时,![]() x
x![]() ,此时函数单增,故A不正确;
,此时函数单增,故A不正确;
周期为![]() ,故B错;
,故B错;
由f(x)≥1即sin(![]() x
x![]() )
)![]() ,可得
,可得![]() 2kπ
2kπ![]() x
x![]() 2kπ
2kπ![]() ,
,
即4kπ≤x≤4kπ![]() ,k∈Z,故C不正确;
,k∈Z,故C不正确;
令![]() x
x![]() kπ,可得x=2kπ
kπ,可得x=2kπ![]() ,k∈Z,即有对称中心为(2kπ
,k∈Z,即有对称中心为(2kπ![]() ,0),故D正确;
,0),故D正确;
故选:D.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案【题目】已知![]() 元集合
元集合![]() 的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为
的一些子集满足:每个子集至少含2个元素,每两个不同子集的交集至多含2个元素,记这些子集的元素个数的立方和为![]() .问:是否存在不小于3的正整数
.问:是否存在不小于3的正整数![]() ,使
,使![]() 的最大值等于2009的方幂?说明你的理由.
的最大值等于2009的方幂?说明你的理由.
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品.
内的产品为合格品,否则为不合格品.
注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量(克) | 频数 |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
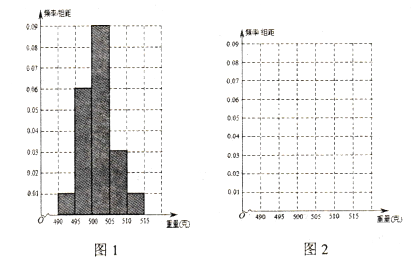
(1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
甲流水线 | 乙流水线 | 合计 | |
合格 | |||
不合格 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期低于平均数的患者,称为“短潜伏者”,潜伏期不低于平均数的患者,称为“长潜伏者”.
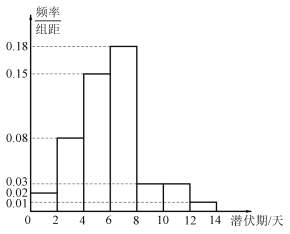
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |