题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆![]() 的离心率可得出
的离心率可得出![]() ,将点
,将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程,可得出
的方程,可得出![]() 和
和![]() 的值,由此可得出椭圆
的值,由此可得出椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,由
的方程联立,由![]() 求出
求出![]() 的范围,列出韦达定理,利用弦长公式计算出
的范围,列出韦达定理,利用弦长公式计算出![]() ,利用点到直线的距离公式求出
,利用点到直线的距离公式求出![]() 的高,然后利用三角形的面积公式结合基本不等式可求出该三角形面积的最大值.
的高,然后利用三角形的面积公式结合基本不等式可求出该三角形面积的最大值.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,![]() .
.
则椭圆![]() 的方程可化为
的方程可化为![]() ,
,
将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程得
的方程得![]() ,可得
,可得![]() ,
,![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立
的方程联立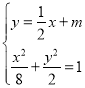 ,
,
消去![]() ,整理得
,整理得![]() ,
,![]() ,得
,得![]() .
.
由韦达定理得![]() ,
,![]() .
.
则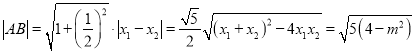 ,
,
直线![]() 的一般方程为
的一般方程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为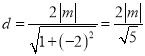 ,
,
所以,![]() ,
,
当且仅当![]() 时,即当
时,即当![]() 时,等号成立,
时,等号成立,
因此,![]() 面积的最大值为
面积的最大值为![]() .
.

 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品.
内的产品为合格品,否则为不合格品.
注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
产品重量(克) | 频数 |
| 6 |
| 8 |
| 14 |
| 8 |
| 4 |
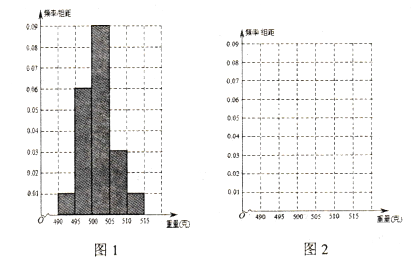
(1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面![]() 列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关.
甲流水线 | 乙流水线 | 合计 | |
合格 | |||
不合格 | |||
合计 |
参考公式:![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期低于平均数的患者,称为“短潜伏者”,潜伏期不低于平均数的患者,称为“长潜伏者”.
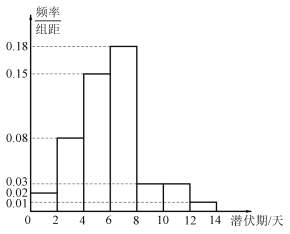
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【题目】为了研究经常使用手机是否对数学学习成绩有影响,某校高二数学研究性学习小组进行了调查,随机抽取高二年级50名学生的一次数学单元测试成绩,并制成下面的2×2列联表:
及格 | 不及格 | 合计 | |
很少使用手机 | 20 | 5 | 25 |
经常使用手机 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
则有( )的把握认为经常使用手机对数学学习成绩有影响.
参考公式: ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.97.5%B.99%C.99.5%D.99.9%