Question

【题目】试求所有的正数 ，使得在双曲线的右支上总存在焦点弦，它关于原点的张角为直角。

Answer 1

【答案】

【解析】

记双曲线的右焦点为，其中，，设焦点弦交双曲线的右支于点.

由，得.①

如果，则渐近线的倾角.而双曲线的右支含于两渐近线所夹的角形区域内，该角形区域的顶角.此时，双曲线右支中的任一条弦关于原点的张角皆小于，不合题意.故.

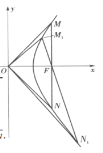
（1）当焦点弦与轴垂直时，若构成以为斜边的直角三角形，则是等腰直角三角形，于是，，（如图），即点满足，而.

由，得.

故.

而，则.

（2）当焦点弦与轴不垂直时，焦点弦与双曲线右支的两个交点具有不同的横坐标，

设的方程为.

将双曲线的方程改写为.

则，即. ②

又方程②有两个不同的正根，则.

由方程②得.

据式①由

，

即.

注意到，则.③

由于，故.

所以， .

又，由式③得，即.

综合（1）、（2），的取值范围是.