题目内容
13.过原点的直线MM′与椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)分别交于点M和点M′,点F2(1,0)是椭圆C的右焦点,且|MF2|=1,|M′F2|=3.(1)求椭圆的方程;
(2)过直线x=4上一点Q作椭圆C的切线,切点为P,求证:以PQ为直径的圆过定点N(1,0)
分析 (1)由已知得a2=b2+c2,c=1,2a=4,由此能求出椭圆C的方程;
(2)设PQ的方程为y=kx+m,代入椭圆方程,消元可得(4k2+3)x2+8kmx+4m2-12=0,由动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),得P(-$\frac{4k}{m}$,$\frac{3}{m}$),由$\left\{\begin{array}{l}{y=kx+m}\\{x=4}\end{array}\right.$,得Q(4,4k+m),证明kPN•kQN=$\frac{\frac{3}{m}}{-\frac{4k}{m}-1}$$•\frac{4k+m}{3}$=-1,即可得出以PQ为直径的圆经过点N(1,0)
解答 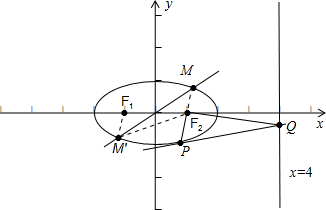 解:(1)由于点F2(1,0)是椭圆C的右焦点,则椭圆的左焦点为F1(-1,0)即c=1,
解:(1)由于点F2(1,0)是椭圆C的右焦点,则椭圆的左焦点为F1(-1,0)即c=1,
又由过原点的直线MM′与椭圆C分别交于点M和点M′,|MF2|=1,|M′F2|=3.
则|MF2|=|M′F1|=1,得到|M′F1|+|M′F2|=2a=4,即a=2.
则b2=4-1=3,故椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设PQ的方程为y=kx+m,代入椭圆方程,消元可得(4k2+3)x2+8kmx+4m2-12=0,
∵动直线l:y=kx+m与椭圆E有且只有一个公共点P(x0,y0),
∴m≠0,△=0,
∴(8km)2-4×(4k2+3)×(4m2-12)=0,
∴4k2-m2+3=0,①
此时x0=$\frac{-4km}{4{k}^{2}+3}$=-$\frac{4k}{m}$,y0=$\frac{3}{m}$,即P(-$\frac{4k}{m}$,$\frac{3}{m}$)
由$\left\{\begin{array}{l}{y=kx+m}\\{x=4}\end{array}\right.$,得Q(4,4k+m),
∴kPN•kQN=$\frac{\frac{3}{m}}{-\frac{4k}{m}-1}$$•\frac{4k+m}{3}$=-1,
∴以PQ为直径的圆过定点N(1,0).
点评 本题考查椭圆C的标准方程的求法,考查以PQ为直径的圆经过点N的判断与求法,解题时要注意函数与方程思想的合理运用.

 智慧小复习系列答案
智慧小复习系列答案| A. | 极大值5,无极小值 | B. | 极大值5,极小值-11 | ||
| C. | 极大值5,极小值-27 | D. | 极小值-27,无极大值 |
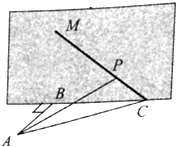 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小.若BC=10m,AC=20m,∠BCM=45°,则tanθ的最大值为$\frac{2\sqrt{3}}{3}$.(仰角θ为直线AP与平面ABC所成角)