题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的一段图象如下所示.
)的一段图象如下所示. 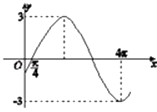
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
【答案】
(1)解:由图象可以得到函数f(x)的振幅A=3,
设函数周期为T,则 ![]() ,
,
所以T=5π,则ω= ![]() ,
,
由ωx0+Φ=0,得 ![]() Φ=0,所以Φ=﹣
Φ=0,所以Φ=﹣ ![]() ,
,
所以f(x)=3sin ![]()
(2)解:由 ![]() ,
,
得 ![]() ,
,
所以函数的减区间为( ![]() +5kπ,4π+5kπ)k∈Z.
+5kπ,4π+5kπ)k∈Z.
函数f(x)的最大值为3,当且仅当 ![]() ,
,
即 ![]() 时函数取得最大值.
时函数取得最大值.
所以函数的最大值为3,取得最大值时的x的集合为{x|x= ![]() }
}
【解析】(1)由图象直接得到振幅A,和四分之三周期,所以周期可求,则ω可求,然后根据五点作图的第一点求得Φ,则函数解析式可求;(2)直接由三角函数符号后面的相位在正弦函数的减区间内求得函数的减区间,由终边在y轴正半轴上的角的正弦值最大求出使函数取得最大值时的角x的集合.
【考点精析】通过灵活运用正弦函数的单调性和三角函数的最值,掌握正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;函数
上是减函数;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 即可以解答此题.
即可以解答此题.

练习册系列答案
相关题目

