题目内容
【题目】下列四组函数中，表示同一函数的是（ ）
A.f（x）=2﹣x ， g（x）=x﹣2
B.
C.
D.
【答案】B
【解析】解：对于A，函数f（x）=2﹣x= 
，与g（x）=x﹣2= 
的对应关系不同，不是同一函数；
对于B，函数f（x）=|x|，与g（x）= 
=|x|的定义域均为R，对应关系也相同，是同一函数；
对于C，函数f（x）= 
=x+1（x≠1），与g（x）=x+1（x∈R）的定义域不同，不是同一函数；
对于D，函数f（x）= 
= 
（x≥1），与y= （x≤﹣1或x≥1）的定义域不同，不是同一函数．
故选：B．
【考点精析】根据题目的已知条件，利用判断两个函数是否为同一函数的相关知识可以得到问题的答案，需要掌握只有定义域和对应法则二者完全相同的函数才是同一函数．
快乐暑假暑假能力自测中西书局系列答案
【题目】某农科所发现，一种作物的年收获量 
（单位： 
）与它“相近”作物的株数 
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 
)，并分别记录了相近作物的株数为 
时，该作物的年收获量的相关数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求该作物的年收获量 
关于它“相近”作物的株数
的线性回归方程；
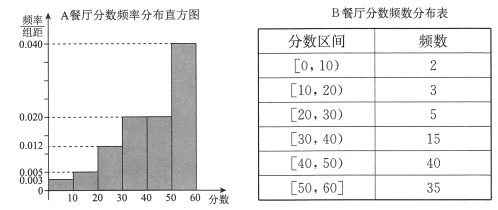
（2）农科所在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每
个小正方形的面积为 
，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．(注:年收
获量以线性回归方程计算所得数据为依据)
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估
计分别为,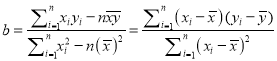 
, 
【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ 
）的一段图象如下所示．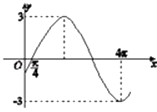 
（1）求f（x）的解析式；
（2）求f（x）的单调减区间，并指出f（x）的最大值及取到最大值时x的集合．
【题目】某公司2016年前三个月的利润（单位：百万元）如下：
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
（1）求利润
关于月份
的线性回归方程；
（2）试用（1）中求得的回归方程预测4月和5月的利润；
（3）试用（1）中求得的回归方程预测该公司2016年从几月份开始利润超过1000万？
相关公式：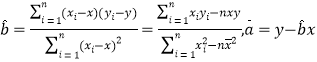
.