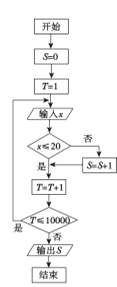
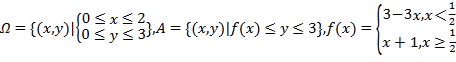题目内容
【题目】已知等比数列{an}的前n项和Sn , 首项a1=a,公比为q(q≠0且q≠1).
(1)推导证明:Sn= ![]() ;
;
(2)等比数列{an}中,是否存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列?若存在,求出符合条件的等比数列公比q的值,若不存在,说明理由;
(3)本题中,若a=q=2,已知数列{nan}的前n项和Tn , 是否存在正整数n,使得Tn≥2016?若存在,求出n的取值集合;若不存在,请说明理由.
【答案】
(1)解:∵Sn=a1+a2+a3+…+an=a1+a1q+a1q2+…+a1qn﹣1,①
∴qSn=a1q+a1q2+a1q3+…+a1qn,②
①﹣②可得(1﹣q)Sn=a1﹣a1qn,
当q≠1时,上式两边同除以1﹣q可得Sn= ![]()
(2)解:不存在存在连续的三项:ak、ak+1、ak+2,使得这三项成等差数列.
证明如下:若ak、ak+1、ak+2成等差数列,则: ![]()
∵ak≠0∴q2﹣q+1=0
而 ![]()
∴不存在存在连续的三项:ak、ak+1、ak+2,使得这三项成等差数列
(3)解:Tn=1×21+2×22+…+n×2n①
2Tn=1×22+2×23+3×24+…+n×2n+1 ②
① ﹣②得Tn=n×2n+1﹣(21+22+23+…+2n)=(n﹣1)2n+1+2
由于Tn是递增的,当n=7时 ![]() ;
;
当n=8时 ![]() .
.
所以存在正整数n,使得Tn≥2016的取值集合为{n|n≥8,n∈N+}
【解析】(1)利用错位相减法真假求解即可.(2)不存在存在连续的三项:ak、ak+1、ak+2 , 使得这三项成等差数列.利用等差数列的等差中项列出关系式,推出矛盾结果.(3)利用错位相减法求出前n项和,通过数列的单调性判断n=7与8时,推出结果即可.
【考点精析】掌握等比数列的基本性质是解答本题的根本,需要知道{an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的一段图象如下所示.
)的一段图象如下所示. 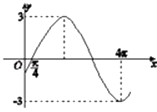
(1)求f(x)的解析式;
(2)求f(x)的单调减区间,并指出f(x)的最大值及取到最大值时x的集合.
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: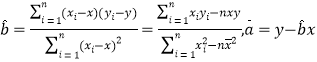 .
.