题目内容
下列说法正确的个数是( )
①正切函数在定义域上单调递增;
②函数f(x)在区间(a,b)上满足f(a)f(b)<0,则函数f(x)在(a,b)上有零点;
③f(x)=log2(x+
)的图象关于原点对称;
④若一个函数是周期函数,那么它一定有最小正周期.
①正切函数在定义域上单调递增;
②函数f(x)在区间(a,b)上满足f(a)f(b)<0,则函数f(x)在(a,b)上有零点;
③f(x)=log2(x+
| x2+1 |
④若一个函数是周期函数,那么它一定有最小正周期.
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:由正切函数的图象可知正确函数在整个定义域上不单调,有无数个单调增区间;
若f(a)f(b)<0,但函数在两端点处不连续,则不一定在(a,b)上有零点;
由定义判断出f(x)=log2(x+
)是奇函数说明③正确;
举例说明④错误.
若f(a)f(b)<0,但函数在两端点处不连续,则不一定在(a,b)上有零点;
由定义判断出f(x)=log2(x+
| x2+1 |
举例说明④错误.
解答:
解:①正切函数在定义域上单调递增,错误,正确函数在整个定义域上不单调,有无数个单调增区间;
②函数f(x)在区间(a,b)上满足f(a)f(b)<0,则函数f(x)在(a,b)上有零点,错误,若函数在两端点处不连续,则不一定在(a,b)上有零点;
③函数f(x)=log2(x+
)的定义域为R,且f(-x)=log2(-x+
)=log2(-x+
)=log2(x+
)-1=-log2(x+
)=-f(x),
∴f(x)为奇函数,图象关于原点对称,正确;
④若一个函数是周期函数,那么它一定有最小正周期,错误,例如常数函数f(x)=1是周期函数,但无最小正周期.
∴正确的命题是③.
故选:B.
②函数f(x)在区间(a,b)上满足f(a)f(b)<0,则函数f(x)在(a,b)上有零点,错误,若函数在两端点处不连续,则不一定在(a,b)上有零点;
③函数f(x)=log2(x+
| x2+1 |
| (-x)2+1 |
| x2+1 |
| x2+1 |
| x2+1 |
∴f(x)为奇函数,图象关于原点对称,正确;
④若一个函数是周期函数,那么它一定有最小正周期,错误,例如常数函数f(x)=1是周期函数,但无最小正周期.
∴正确的命题是③.
故选:B.
点评:本题考查了命题的真假判断与应用,考查了函数的性质,考查了函数零点的判定方法,是中档题.

练习册系列答案
相关题目
设抛物线y2=8x上一点P到直线x=-2的距离是6,则点P到该抛物线焦点的距离是( )
| A、12 | B、8 | C、6 | D、4 |
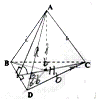 如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.
如图,已知空间四边形ABCD,及两条对角线AC、BD,AB=AC=AD=a,BD=DC=CD=b,AB⊥面BCD,垂足为H,求平面ABD与平面BCD所成角的大小.