题目内容
8.g(x)=$\sqrt{2}$2x-1,g(x)≤t2-2mt+1对所有的x∈[-1,1]及m∈[-1,1]恒成立,求实数t的取值范围.分析 化简g(x)=$\sqrt{2}$2x-1=2x-1;从而求得gmax(x)=g(1)=2-1=1;从而化恒成立为2mt≤t2对所有的m∈[-1,1]恒成立;再讨论t以化为函数的最值问题即可.
解答 解:g(x)=$\sqrt{2}$2x-1=2x-1;
故gmax(x)=g(1)=2-1=1;
故g(x)≤t2-2mt+1对所有的x∈[-1,1]及m∈[-1,1]恒成立可化为
1≤t2-2mt+1对所有的m∈[-1,1]恒成立;
即2mt≤t2对所有的m∈[-1,1]恒成立;
当t=0时,2mt≤t2对所有的m∈[-1,1]恒成立;
当t<0时,m≥$\frac{t}{2}$对所有的m∈[-1,1]恒成立;
故$\frac{t}{2}$≤-1,即t≤-2;
当t>0时,m≤$\frac{t}{2}$对所有的m∈[-1,1]恒成立;
故$\frac{t}{2}$≥1,即t≥2;
综上所述,实数t的取值范围为
(-∞,-2]∪{0}∪[2,+∞).
点评 本题考查了恒成立问题,同时考查了分类讨论的思想应用,属于中档题.

练习册系列答案
相关题目
8.设z1,z2∈C,则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
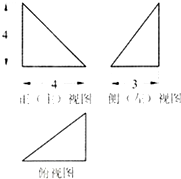 某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.
某四面体的三视图如图所示,该四面体的体积是8,该四面体四个面的面积中最大的是10.