题目内容
3.在正方体ABCD-A1B1C1D1中,P为CD的中点,M为CC1的中点,N为BC的中点.(1)求证:A1P⊥DN;
(2)求证:A1PA⊥平面MND;
(3)求二面角M-DN-C的正切值.
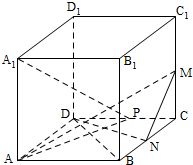
分析 (1)根据线面垂直的性质证明DN⊥平面A1AP即可证明A1P⊥DN;
(2)根据面面垂直的判定定理即可证明A1PA⊥平面MND;
(3)根据二面角的定义作出二面角的平面角,根据三角形的边角关系即可求二面角M-DN-C的正切值.
解答 证明:(1)∵P为CD的中点,N为BC的中点.
∴DP=CN,AD=DC,AP=DN,
则△ADB≌△DCN,
则∠DPA=∠CND,
即OPCN四点共圆,
则以PN为直径,则∠PON=90°,
即DN⊥AP,
∵A1A⊥平面ABCD;
∴A1A⊥DN,
∵A1A∩AP=A,
∴DN⊥平面A1AP,
∵A1P?平面A1AP,
∴DN⊥A1P,
即A1P⊥DN;
(2)由(1)知DN⊥平面A1AP,DN?平面MND,
∴平面A1PA⊥平面MND;
(3)∵C1C⊥平面ABCD;
∴过C作CH⊥DN于H,连接C1H,
则C1H⊥DN,
即∠C1HC是二面角M-DN-C的平面角,
设正方体的棱长为2,则CM=1,CD=2,CN=1,
则DN=$\sqrt{5}$,
∵CH•DN=CD•CN,
∴CH=$\frac{CD•CN}{DN}$=$\frac{2×1}{\sqrt{5}}$=$\frac{2}{\sqrt{5}}$,
则二面角M-DN-C的正切值tan∠C1HC=$\frac{CM}{CH}$=$\frac{1}{\frac{2}{\sqrt{5}}}$=$\frac{\sqrt{5}}{2}$.
点评 本题主要考查空间线面垂直的性质以及面面垂直的判定,以及二面角的求解,根据相应的判定定理以及作出二面角的平面角是解决本题的关键.考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知点A的坐标为(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{3}$至OB,则点B的纵坐标为( )
| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{3}}}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{13}{2}$ |
15.已知a>0且a≠1,命题“?x>1,logax>0”的否定是( )
| A. | ?x≤1,logax>0 | B. | ?x>1,loga≤0 | C. | ?x≤1,logax>0 | D. | ?x>1,logax≤0 |
13.直角三角形ABC中,A为直角,AB=1,BC=2,若点AM是BC边上的高线,点P在△ABC 内部或边界上运动,则$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是( )
| A. | [-$\frac{\sqrt{3}}{2}$,0] | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{\sqrt{3}}{4}$,0] | D. | [-3,0] |