题目内容
19.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,左、右焦点分别为F1,F2,抛物线y2=4$\sqrt{2}$x的焦点F恰好是椭圆C的一个顶点.(1)求椭圆C的方程;
(2)已知圆O:x2+y2=$\frac{2}{3}$的切线l与椭圆相交于A,B两点,证明:以AB为直径的圆必经过原点.
分析 (1)通过$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$、抛物线y2=4$\sqrt{2}$x的焦点F恰好是椭圆C的一个顶点,计算即得结论;
(2)分直线l的斜率不存在、直线l的斜率为0、直线l的斜率存在且不为0三种情况讨论,利用韦达定理计算即得结论.
解答 (1)解:∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,即a=$\sqrt{2}$c,
∵抛物线y2=4$\sqrt{2}$x的焦点F恰好是椭圆C的一个顶点,
∴a=$\sqrt{2}$,∴c=b=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)证明:①当直线l的斜率不存在时,
∵直线l与圆O相切,∴直线方程为:x=$\frac{\sqrt{6}}{3}$或x=-$\frac{\sqrt{6}}{3}$,
Ⅰ.联立$\frac{{x}^{2}}{2}+{y}^{2}=1$与x=$\frac{\sqrt{6}}{3}$,可得:A($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),B($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),
∴以AB为直径的圆的方程为:(x-$\frac{\sqrt{6}}{3}$)2+y2=$\frac{2}{3}$;
Ⅱ.联立$\frac{{x}^{2}}{2}+{y}^{2}=1$与x=-$\frac{\sqrt{6}}{3}$,可得:A(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),B(-$\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),
∴以AB为直径的圆的方程为:(x+$\frac{\sqrt{6}}{3}$)2+y2=$\frac{2}{3}$;
综合Ⅰ、Ⅱ可知两圆过定点(0,0);
②当直线l的斜率为0时,
∵直线l与圆O相切,∴切线方程为:y=$\frac{\sqrt{6}}{3}$或y=-$\frac{\sqrt{6}}{3}$,
Ⅰ.联立$\frac{{x}^{2}}{2}+{y}^{2}=1$与y=-$\frac{\sqrt{6}}{3}$,可得:A($\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),B(-$\frac{\sqrt{6}}{3}$,-$\frac{\sqrt{6}}{3}$),
∴以AB为直径的圆的方程为:x2+(y+$\frac{\sqrt{6}}{3}$)2=$\frac{2}{3}$;
Ⅱ.联立$\frac{{x}^{2}}{2}+{y}^{2}=1$与y=$\frac{\sqrt{6}}{3}$,可得:A($\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),B(-$\frac{\sqrt{6}}{3}$,$\frac{\sqrt{6}}{3}$),
∴以AB为直径的圆的方程为:x2+(y-$\frac{\sqrt{6}}{3}$)2=$\frac{2}{3}$;
综合Ⅰ、Ⅱ,显然过定点(0,0);
③当直线l的斜率存在且不为0时,联立$\frac{{x}^{2}}{2}+{y}^{2}=1$与y=kx+m,
消去y得:(1+2k2)x2+4kmx+2m2-2=0,
设A(x1,y1),B(x2,y2),
由韦达定理知:x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
∴y1y2=$\frac{{m}^{2}-2{k}^{2}}{1+2{k}^{2}}$,$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=$\frac{3{m}^{2}-2{k}^{2}-2}{1+2{k}^{2}}$,
∵直线与圆相切,∴圆心到直线的距离d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{6}}{3}$,
即m2=$\frac{2}{3}$(1+k2),从而$\overrightarrow{OA}•\overrightarrow{OB}$=0,
显然以AB为直径的圆经过原点;
综合①②③可知:以AB为直径的圆必经过原点.
点评 本题考查求椭圆方程,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | m∈(-$\frac{1}{2}$,+∞) | B. | m∈(-$\frac{1}{2}$,1) | C. | m∈[-$\frac{1}{2}$,+∞) | D. | m∈[-$\frac{1}{2}$,1) |
 某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )
某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )| A. | 102 | B. | 104 | C. | 112 | D. | 114 |
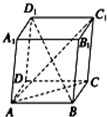 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |