题目内容

18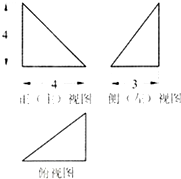．某四面体的三视图如图所示，该四面体的体积是8，该四面体四个面的面积中最大的是10．

分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，求出底面面积，代入棱锥体积公式，可得答案．

解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，
其直观图如下图所示：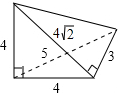

底面面积S=$\frac{1}{2}$×3×4=6，
棱柱的高h=4，
故棱柱的体积V=$\frac{1}{3}$Sh=8，
三棱锥四面面的面积分别为：8，6，6$\sqrt{2}$，10
显然面积的最大值为10
故答案为：8；10．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
8．g（x）=$\sqrt{2}$2x-1，g（x）≤t2-2mt+1对所有的x∈[-1，1]及m∈[-1，1]恒成立，求实数t的取值范围．
9．设函数f（x）=lnx，h（x）=f（x）+mf′（x）．
（1）求函数h（x）单调区间；
（2）当m=e（e为自然对数的底数）时，若h（n）-h（x）＜$\frac{e}{n}$对?x＞0恒成立，求实数n的取值范围．
6．在平面直角坐标系xOy中，已知曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=\sqrt{5}sinα}\end{array}\right.$（α为参数），以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标轴方程为ρcos（θ-$\frac{π}{4}$）=2$\sqrt{2}$．
（1）求曲线C的普通方程与直线l的直角坐标方程；
（2）设点P为曲线C上的动点，求点P到直线l距离的最大值及其对应的点P的直角坐标．
13．直角三角形ABC中，A为直角，AB=1，BC=2，若点AM是BC边上的高线，点P在△ABC 内部或边界上运动，则$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是（　　）
A．[-$\frac{\sqrt{3}}{2}$，0]B．[-$\frac{3}{4}$，0]C．[-$\frac{\sqrt{3}}{4}$，0]D．[-3，0]
3．已知函数f（x）和g（x）的图象关于原点对称，f（x）=x2+2x．
（1）若函数h（x）=$\frac{1}{2}$f（x）-x-|2x-a|有四个不同零点，求实数a的取值范围
（2）如果对于任意x∈R，不等式g（x）+c≤f（x）-|x-1|恒成立，求实数c的取值范围．
10．设不等式组$\left\{\begin{array}{l}{x+y-3≥0}\\{2x-y≥0}\\{x-2≤0}\end{array}\right.$，表示的平面区域为D，若直线mx+y+m=0上存在区域D上的点，则实数m的取值范围是$-\frac{4}{3}≤m≤-\frac{1}{3}$．
7．已知点F（c，0），A分别为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点和上顶点，点B为直线l：x=$\frac{{a}^{2}}{c}$上一动点，且△ABF的外接圆面积最小值为4π，则当椭圆的短轴最长时，椭圆的离心率为$\frac{\sqrt{2}}{2}$．
8．若集合U={2，0，1，3，4，5}，集合A={0，3，4，2}，B={0，1，2，3，4}，则∁U（A∩B）=（　　）
A．{0，3，4，2}B．{0，2}C．{1，5}D．{2，0，1，5}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网