题目内容
17.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=100$\sqrt{6}$m.
分析 设此山高h(m),在△BCD中,利用仰角的正切表示出BC,进而在△ABC中利用正弦定理求得h.
解答 解:设此山高h(m),则BC=$\sqrt{3}$h,
在△ABC中,∠BAC=30°,∠CBA=105°,∠BCA=45°,AB=600.
根据正弦定理得$\frac{\sqrt{3}h}{sin30°}$=$\frac{600}{sin45°}$,
解得h=100$\sqrt{6}$(m)
故答案为:100$\sqrt{6}$.
点评 本题主要考查了解三角形的实际应用.关键是构造三角形,将各个已知条件向这个主三角形集中,再通过正弦、余弦定理或其他基本性质建立条件之间的联系,列方程或列式求解.

练习册系列答案
相关题目
8.“sinα=cosα”是“cos2α=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.Sn为数列{an}的前n项和,己知an>0,an2+2an=4Sn+3
(I)求{an}的通项公式:
(Ⅱ)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{bn}的前n项和.
(I)求{an}的通项公式:
(Ⅱ)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{bn}的前n项和.
12.在区间[0,1]上随机取两个数x,y,记p1为事件“x+y≤$\frac{1}{2}$”的概率,P2为事件“xy≤$\frac{1}{2}$”的概率,则( )
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
9.过三点A(1,0),B(0,$\sqrt{3}$),C(2,$\sqrt{3}$)则△ABC外接圆的圆心到原点的距离为( )
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{21}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\frac{4}{3}$ |
9.一个四面体的三视图如图所示,则该四面体的表面积是( )
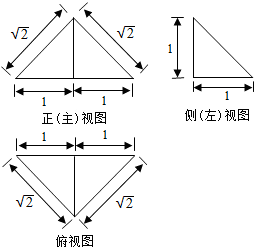

| A. | 1+$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.