题目内容
7. 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线AF与平面α所成角的正弦值.
分析 (1)容易知道所围成正方形的边长为10,再结合长方体各边的长度,即可找出正方形的位置,从而画出这个正方形;
(2)分别以直线DA,DC,DD1为x,y,z轴,建立空间直角坐标系,考虑用空间向量解决本问,能够确定A,H,E,F几点的坐标.设平面EFGH的法向量为$\overrightarrow{n}=(x,y,z)$,根据$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EH}=0}\\{\overrightarrow{n}•\overrightarrow{EF}=0}\end{array}\right.$即可求出法向量$\overrightarrow{n}$,$\overrightarrow{AF}$坐标可以求出,可设直线AF与平面EFGH所成角为θ,由sinθ=$|cos<\overrightarrow{n},\overrightarrow{AF}>|$即可求得直线AF与平面α所成角的正弦值.
解答 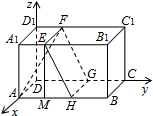 解:(1)交线围成的正方形EFGH如图:
解:(1)交线围成的正方形EFGH如图:
(2)作EM⊥AB,垂足为M,则:
EH=EF=BC=10,EM=AA1=8;
∴$MH=\sqrt{E{H}^{2}-E{M}^{2}}=6$,∴AH=10;
以边DA,DC,DD1所在直线为x,y,z轴,建立如图所示空间直角坐标系,则:
A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8);
∴$\overrightarrow{EF}=(-10,0,0),\overrightarrow{EH}=(0,6,-8)$;
设$\overrightarrow{n}=(x,y,z)$为平面EFGH的法向量,则:
$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=-10x=0}\\{\overrightarrow{n}•\overrightarrow{EH}=6y-8z=0}\end{array}\right.$,取z=3,则$\overrightarrow{n}=(0,4,3)$;
若设直线AF和平面EFGH所成的角为θ,则:
sinθ=$|cos<\overrightarrow{AF},\overrightarrow{n}>|$=$\frac{40}{\sqrt{180}•5}=\frac{4\sqrt{5}}{15}$;
∴直线AF与平面α所成角的正弦值为$\frac{4\sqrt{5}}{15}$.
点评 考查直角三角形边的关系,通过建立空间直角坐标系,利用空间向量解决线面角问题的方法,弄清直线和平面所成角与直线的方向向量和平面法向量所成角的关系,以及向量夹角余弦的坐标公式.

| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{4}$-y2=1 | C. | $\frac{{y}^{2}}{4}$-x2=1 | D. | y2-$\frac{{x}^{2}}{4}$=1 |
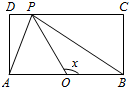 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 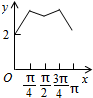 | B. | 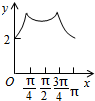 | C. | 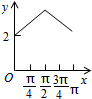 | D. | 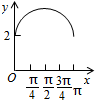 |

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | $\frac{5}{21}$ | B. | $\frac{10}{21}$ | C. | $\frac{11}{21}$ | D. | 1 |
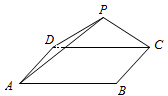 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3.
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=PC=4,AB=6,BC=3. 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,