题目内容
12.在区间[0,1]上随机取两个数x,y,记p1为事件“x+y≤$\frac{1}{2}$”的概率,P2为事件“xy≤$\frac{1}{2}$”的概率,则( )| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
分析 分别求出事件“x+y≤$\frac{1}{2}$”和事件“xy≤$\frac{1}{2}$”对应的区域,然后求出面积,利用几何概型公式求出概率,比较大小.
解答 解:由题意,事件“x+y≤$\frac{1}{2}$”表示的区域如图阴影三角形,
p1=$\frac{\frac{1}{2}×\frac{1}{2}×\frac{1}{2}}{1}=\frac{1}{8}$;
满足事件“xy≤$\frac{1}{2}$”的区域如图阴影部分
所以p2=$\frac{1×\frac{1}{2}+{∫}_{\frac{1}{2}}^{1}\frac{1}{2x}dx}{1}$=$\frac{1}{2}+\frac{1}{2}lnx{|}_{\frac{1}{2}}^{1}$=$\frac{1}{2}(1+ln2)$>$\frac{1}{2}$;
所以${p}_{1}<\frac{1}{2}<{p}_{2}$;
故选:B.
点评 本题考查了几何概型的公式运用;关键是分别求出阴影部分的面积,利用几何概型公式解答.

练习册系列答案
相关题目
2.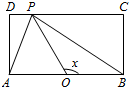 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
 如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )
如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,记∠BOP=x.将动点P到A,B两点距离之和表示为x的函数f(x),则y=f(x)的图象大致为( )| A. | 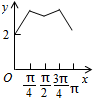 | B. | 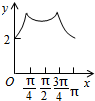 | C. | 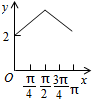 | D. | 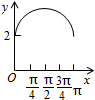 |
20.已知M(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的左、右两个焦点,若$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$<0,则y0的取值范围是( )
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
7.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
| A. | 134石 | B. | 169石 | C. | 338石 | D. | 1365石 |
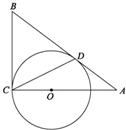 如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.