题目内容
9.过三点A(1,0),B(0,$\sqrt{3}$),C(2,$\sqrt{3}$)则△ABC外接圆的圆心到原点的距离为( )| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{21}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\frac{4}{3}$ |
分析 利用外接圆的性质,求出圆心坐标,再根据圆心到原点的距离公式即可求出结论.
解答 解:因为△ABC外接圆的圆心在直线BC垂直平分线上,即直线x=1上,
可设圆心P(1,p),由PA=PB得
|p|=$\sqrt{1{+(p-\sqrt{3})}^{2}}$,
得p=$\frac{2\sqrt{3}}{3}$
圆心坐标为P(1,$\frac{2\sqrt{3}}{3}$),
所以圆心到原点的距离|OP|=$\sqrt{1+(\frac{2\sqrt{3}}{3})^{2}}$=$\sqrt{1+\frac{12}{9}}$=$\frac{\sqrt{21}}{3}$,
故选:B
点评 本题主要考查圆性质及△ABC外接圆的性质,了解性质并灵运用是解决本题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
20.已知M(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的左、右两个焦点,若$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$<0,则y0的取值范围是( )
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
1.设变量x,y满足约束条件$\left\{\begin{array}{l}x+2≥0\\ x-y+3≥0\\ 2x+y-3≤0\end{array}\right.$,则目标函数z=x+6y的最大值为( )
| A. | 3 | B. | 4 | C. | 18 | D. | 40 |
18.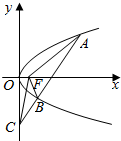 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
 如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )
如图,设抛物线y2=4x的焦点为F,不经过焦点的直线上有三个不同的点A,B,C,其中点A,B在抛物线上,点C在y轴上,则△BCF与△ACF的面积之比是( )| A. | $\frac{{|{BF}|-1}}{{|{AF}|-1}}$ | B. | $\frac{{{{|{BF}|}^2}-1}}{{{{|{AF}|}^2}-1}}$ | C. | $\frac{{|{BF}|+1}}{{|{AF}|+1}}$ | D. | $\frac{{{{|{BF}|}^2}+1}}{{{{|{AF}|}^2}+1}}$ |

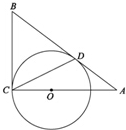 如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.
如图,AB和BC分别与圆O相切于点D、C,AC经过圆心O,且BC=2OC.