题目内容
5.Sn为数列{an}的前n项和,己知an>0,an2+2an=4Sn+3(I)求{an}的通项公式:
(Ⅱ)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{bn}的前n项和.
分析 (I)根据数列的递推关系,利用作差法即可求{an}的通项公式:
(Ⅱ)求出bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,利用裂项法即可求数列{bn}的前n项和.
解答 解:(I)由an2+2an=4Sn+3,可知an+12+2an+1=4Sn+1+3
两式相减得an+12-an2+2(an+1-an)=4an+1,
即2(an+1+an)=an+12-an2=(an+1+an)(an+1-an),
∵an>0,∴an+1-an=2,
∵a12+2a1=4a1+3,
∴a1=-1(舍)或a1=3,
则{an}是首项为3,公差d=2的等差数列,
∴{an}的通项公式an=3+2(n-1)=2n+1:
(Ⅱ)∵an=2n+1,
∴bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$($\frac{1}{2n+1}$-$\frac{1}{2n+3}$),
∴数列{bn}的前n项和Tn=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$$+\frac{1}{5}$$-\frac{1}{7}$+…+$\frac{1}{2n+1}$-$\frac{1}{2n+3}$)=$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{2n+3}$)=$\frac{n}{3(2n+3)}$.
点评 本题主要考查数列的通项公式以及数列求和的计算,利用裂项法是解决本题的关键.

练习册系列答案
相关题目
16.袋中共有15个除了颜色外完全相同的球,其中有10个白球,5个红球.从袋中任取2个球,所取的2个球中恰有1个白球,1个红球的概率为( )
| A. | $\frac{5}{21}$ | B. | $\frac{10}{21}$ | C. | $\frac{11}{21}$ | D. | 1 |
20.已知M(x0,y0)是双曲线C:$\frac{{x}^{2}}{2}-{y}^{2}$=1上的一点,F1,F2是C的左、右两个焦点,若$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$<0,则y0的取值范围是( )
| A. | $(-\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$ | B. | $(-\frac{\sqrt{3}}{6},\frac{\sqrt{3}}{6})$ | C. | $(-\frac{2\sqrt{2}}{3},\frac{2\sqrt{2}}{3})$ | D. | $(-\frac{2\sqrt{3}}{3},\frac{2\sqrt{3}}{3})$ |
10.l1,l2表示空间中的两条直线,若p:l1,l2是异面直线,q:l1,l2不相交,则( )
| A. | p是q的充分条件,但不是q的必要条件 | |
| B. | p是q的必要条件,但不是q的充分条件 | |
| C. | p是q的充分必要条件 | |
| D. | p既不是q的充分条件,也不是q的必要条件 |
 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点,
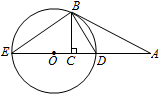 如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.
如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.