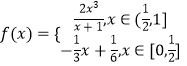题目内容
【题目】已知
是定义在(0,+∞)上的增函数,且满足
＝
＋
＝1.
(1)求证: 
＝3;
(2)求不等式
>3的解集.
【答案】（1）
（2）{x|2< 
<
}
【解析】试题分析：（1）本小题应用赋值法可求得
，令
，得
，令
，得
；（2）解此不等式，必须利用函数为减函数的性质，因此把不等式
变为
，即为
，由减函数定义有
，再结合函数定义域可得不等式的解集．
试题解析：（1）证明： 由题意得
f（8）＝f（4×2）＝f（4）＋f（2）＝f（2×2）＋f（2）＝f（2）＋f（2）＋f（2）＝3f（2）
又∵f（2）＝1
∴f（8）＝3
（2）解：∵f（8）＝3
∴f（x）>f（x－2）＋f（8）＝f（8x－16）
∵f（x）是（0，+∞）上的减函数
∴
解得
的解集是
练习册系列答案
阅读快车系列答案
相关题目
【题目】某市春节7家超市的广告费支出x（万元）和销售额y（万元）数据如下，
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
（1）请根据上表提供的数据．用最小二乘法求出y关于x的线性回归方程； 
= 
x+ 
（2）用二次函数回归模型拟合y与x的关系，可得回归方程： =﹣0.17x2+5x+20． 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75，请用R2说明选择哪个回归模型更合适．并用此模型预测A超市广告费支出为3万元时的销售额，
参考数据及公式： 
=8， 
=42. 
xiyi=2794， x 
=708， = 
= 
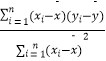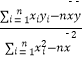， = ﹣ x．
