题目内容
【题目】某商品在最近100天内的价格f(t)与时间t的函数关系式是

销售量g(t)与时间t的函数关系式是g(t)=-![]() +
+![]() (0≤t≤100),求这种商品的日销售额的最大值.
(0≤t≤100),求这种商品的日销售额的最大值.
【答案】日销售额的最大值为808.5.
【解析】试题分析:(1)设日销售额为S,根据已知可得S=-![]()
![]() +
+![]() +
+![]() ×
×![]()
![]() ,S=
,S=![]() (t2-213t+104×109)
(t2-213t+104×109) ![]() ;分别求出最大值,综合讨论可得日销售额的最大值为808.5.
;分别求出最大值,综合讨论可得日销售额的最大值为808.5.
试题解析:
解:设日销售额为S,①当0≤t≤40(t∈N*)时,
S=![]()
![]()
=-![]() (t+88)(t-109)
(t+88)(t-109)
=-![]() (t2-21t-88×109)
(t2-21t-88×109)
=-![]()
![]() +
+![]() +
+![]() ×
×![]() ,
,
当t=10,或t=11时,Smax=808.5.
②当40<t≤100(t∈N*)时,
S=![]()
![]()
=![]() (t-104)(t-109)
(t-104)(t-109)
=![]() (t2-213t+104×109)
(t2-213t+104×109)
为二次函数,它在区间(40,100]上是减函数,因此在靠近左端t=41处取最大值,即当t=41时,Smax=714,由①②知日销售额的最大值为808.5.

练习册系列答案
相关题目
【题目】濮阳市黄河滩区某村2010年至2016年人均纯收入(单位:万元)的数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y关于x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2010年至2016年该村人均纯收入的变化情况,并预测该村2017年人均纯收入.
附:回归直线的斜率和截距的最小乘法估计公式分别为: ![]() =
= 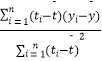 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.