题目内容
【题目】已知函数
有如下性质：如果常数
，那么该函数
上是减函数，在
上是增函数．
（1）用函数单调性定义来证明
上的单调性；
（2）已知
， 
，求函数
的值域；
（3）对于（2）中的函数
和函数
，若对任意
，总存在
，使得
成立，求实数
的值．
【答案】（1）见解析；（2）
；（3）
.
【解析】试题分析：（1）利用单调性的定义证明单调递减；（2）构造函数得
，换元求得值域为
；（3）由（2）知
的值域为
， 
的值域是
的值域的子集，所以
.
试题解析：
（1）证明：设
-
=
-
=
-
-
，
故函数
（2）
，
设
则
则
， 
．
由已知性质得，
当
，即
时， 
单调递减；所以减区间为
；
当
，即
时， 
单调递增；所以增区间为
；
，得
的值域为
（3）由（2）知
的值域为
， 又
为减函数，故
．
由题意知， 
的值域是
的值域的子集，
练习册系列答案
相关题目
【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼，随机抽取50条作为样本进行统计，按海鱼重量（克）得到如图的频率分布直方图：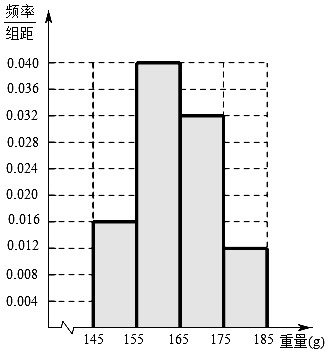 
（Ⅰ）若经销商购进这批海鱼100千克，试估计这批海鱼有多少条（同一组中的数据用该区间的中点值作代表）；
（Ⅱ）根据市场行情，该海鱼按重量可分为三个等级，如下表：
等级 | 一等品 | 二等品 | 三等品 |
重量（g） | [165，185] | [155，165） | [145，155） |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据，视频率为概率．现从这批海鱼中随机抽取3条，记抽到二等品的条数为X，求x的分布列和数学期望．
