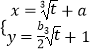题目内容
【题目】已知函数 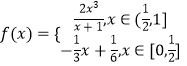 ,函数
,函数 ![]()
![]() (a>0),若存在
(a>0),若存在 ![]() ,使得
,使得 ![]() 成立,则实数
成立,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】∵ 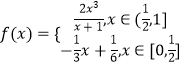 ,
,
① 当x∈[0, ![]() ]时,f(x)=
]时,f(x)= ![]() 在R上是单调递减函数,
在R上是单调递减函数,
∴f( ![]() )f(x)f(0),即0f(x)
)f(x)f(0),即0f(x) ![]() ,
,
∴f(x)的值域为[0, ![]() ];
];
② 当x∈( ![]() ,1]时,f(x)=
,1]时,f(x)= ![]() ,
,
∴f′(x)= ![]() =
= ![]() ,
,
∴当x> ![]() 时,f′(x)>0,即f(x)在(
时,f′(x)>0,即f(x)在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f(x)在( ![]() ,1]上单调递增,
,1]上单调递增,
∴f( ![]() )<f(x)f(1),即
)<f(x)f(1),即 ![]() <f(x)1,
<f(x)1,
∴f(x)的值域为[ ![]() ,1].
,1].
综合①②,f(x)的值域为[0,1].
∵g(x)=asin( ![]() )2a+2,(a>0),且x∈[0,1],
)2a+2,(a>0),且x∈[0,1],
∴0 ![]() x
x ![]() ,则0sin(
,则0sin( ![]() x)
x) ![]() ,
,
∵a>0则0asin( ![]() x)
x) ![]() a,
a,
∴22ag(x)2 ![]() a,
a,
∴g(x)的值域为[22a,2 ![]() a],
a],
∵存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,
∴[0,1]∩[22a,2 ![]() a]≠,
a]≠,
若[0,1]∩[22a,2 ![]() a]=,则2
a]=,则2 ![]() a<0或22a>1,
a<0或22a>1,
∴a< ![]() 或a>
或a> ![]() ,
,
∴当[0,1]∩[22a,2 ![]() a]≠时,a的取值范围为[12,
a]≠时,a的取值范围为[12, ![]() ],
],
∴实数a的取值范围是[ ![]() ,
, ![]() ].
].
故答案为:D.
根据x的范围确定函数的值域和 g(x) 的值域,进而根据f ( x1 ) = g ( x2 ) 成立,推断出[0,1]∩[22a,2 3 2 a]≠时,先看当二者的交集为空集时求得a的范围,故可求得当集合的交集为非空时a的范围。

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
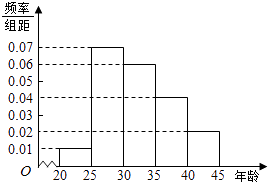
激活思维智能训练课时导学练系列答案【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图: 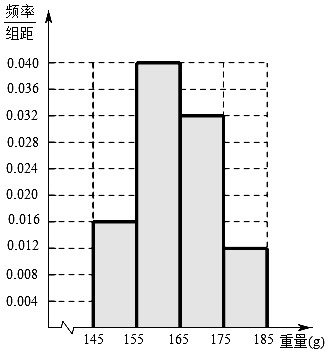
(Ⅰ)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(Ⅱ)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [165,185] | [155,165) | [145,155) |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.